Реферат: Антипростые числа
Для исследования антипростых чисел была разработана программа на Паскале, которая вычисляет антипростые числа. В Приложении А представлена таблица антипростых чисел на отрезке до 
. В принципе программа позволяет повысить значение n до большей величины, а также дает ответ, что среди чисел на отрезке до 
3136000000 троек антипростых чисел вида n - 1, n, n + 1 не найдено.
При исследовании количества антипростых чисел были проведены сравнения значений функции p(n) с функцией
, которые показали, на отрезке до n=420000 
p(n), а далее 
p(n), причём процент ошибки небольшой. Так как вначале p(n), то процент ошибки убывает, после n=420000 он начинает возрастать, и при n=2000000 он приблизительно равен 2%.
При исследовании частоты встречаемости антипростых чисел среди натуральных чисел были проведены сравнения значений функции t(m) с функцией f(m)=
и t(m) с полученной функцией y(x)=
(
) до m= 1500000. Вычислена средняя ошибка приближения. Средняя ошибка приближения функции t(m) к функции f(m)= составила 1,185812%, а к функции y(x)= - 0,280031%.
В обобщениях об антипростых числах были сформулированы и доказаны семь теорем, а также три вопроса.
В заключении следует отметить, что тематика данной исследовательской работы является достаточно новой и поэтому и достаточно интересной.
В дальнейшем планирую продолжать исследовать антипростые числа.
Список использованных источников и литературы
1. Сендеров В., Френкин Б. Гипотеза Каталана. - журнал "Квант", 2007, №4. – С. 8-10 .
2. Сендеров В. Решение задачи М2032. – журнал Квант", 2007, №4. – С. 19-21.
3. Оре О. Приглашение в теорию чисел – Серия "Библиотечка "Квант"", М. 1980. – 128 с.
4. Виноградов И.М. Основы теории чисел. – М.: Наука, 1972. – 168 с.
5. Нестеренко Ю.В. Теория чисел. – М.: Академия, 2008. -273 с.
6. Манин Ю.И., Панчишкин А.А. Теория чисел I. Введение в теорию чисел. – М.: ВИНИТИ, 1989.- 402 с.
Приложение A - +Таблица антипростых чисел
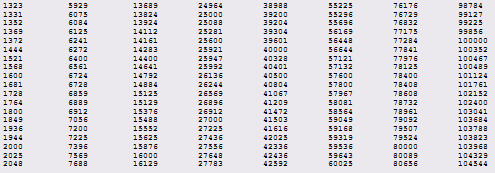
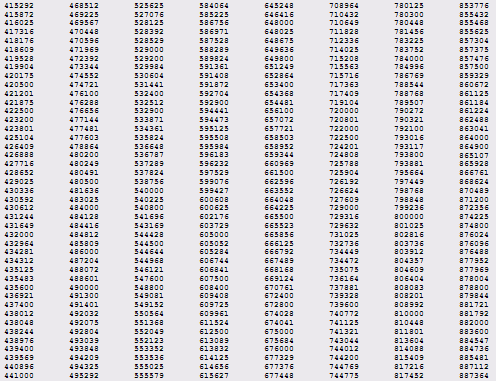
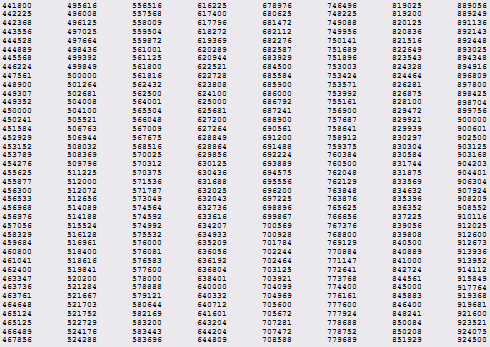
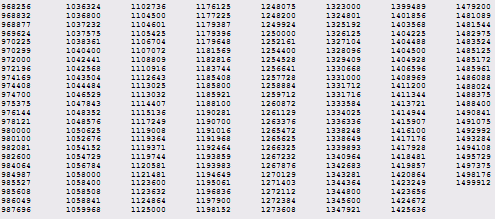
Приложение Б – Программа нахождения антипростых чисел
program Project2;
var
k:real;
b,t,i,j,m,n:longint;
a:array[1..2000000] of longint;
begin