Реферат: Асимптотические методы исследования нестационарных режимов в сетях случайного доступа

Предложенный метод анализа марковизируемых систем [7] обычно имеет два этапа. На первом этапе удается определить асимптотическое среднее исследуемых характеристик системы, а на втором – распределение вероятностей значений отклонений рассматриваемых характеристик от их асимптотических средних.

1. Исследование нестационарной сети случайного доступа с динамическим протоколом в условиях большой загрузки

Рассмотрим спутниковую сеть связи, управляемую динамическим протоколом случайного множественного доступа с оповещением о конфликте. Архитектура такой сети состоит из большого числа территориально-распределенных абонентских станций (АС), которые передают сообщения через геостационарный спутник-ретранслятор. Так как спутниковый канал связи совместно используют все АС, то возможно совпадение времени ретрансляции сообщений от двух или более АС, при этом сообщения искажаются и требуют повторной передачи. Такая ситуация называется конфликтом. Предполагается, что спутник-ретранслятор имеет возможность обнаружения возникающих конфликтов и реализации сигнала оповещения. Абонентские станции способны воспринимать (идентифицировать) сигнал оповещения о конфликте, так, чтобы в каждой АС по прошествии заданного времени распространения сигнала можно было определить, правильно приняты переданные сообщения или нет.

Сообщения, поступающие на спутник-ретранслятор во время распространения сигнала оповещения о конфликте, считаются искаженными. Все искаженные сообщения поступают в источник повторных вызовов (ИПВ). После определения АС того, что посланное сообщение попало в конфликт, АС производит случайную задержку, после которой вновь реализует передачу. В динамическом протоколе предлагается использовать случайную задержку повторной попытки, распределенную экспоненциально с параметром, зависящим от количества сообщений, находящихся в ИПВ. Динамические протоколы, как правило, не реализуемы. Но могут приближенно оценивать функционирование адаптивных протоколов, в которых количество заявок в ИПВ заменяется некоторым оценочным числом.

В качестве математической модели сети связи, управляемой динамическим протоколом случайного множественного доступа с оповещением о конфликте, рассмотрим однолинейную СМО. Прибор (спутник-ретранслятор) может находиться в одном из трех состояний:

Каждая заявка в момент поступления в систему встает на прибор и немедленно начинает обслуживаться. Если за время ее обслуживания другие заявки не поступали, то она после окончания обслуживания покидает систему и в дальнейшем не рассматривается. Если же за время ее обслуживания поступает другая заявка, то возникает конфликтная ситуация и начинается этап оповещения о конфликте, длительность которого распределена по экспоненциальному закону.

Заявки, попавшие в конфликт, а также поступающие в систему во время оповещения о конфликте, автоматически переходят в источник повторных вызовов (ИПВ). Из него они вновь обращаются к прибору с попыткой повторного обслуживания через случайные интервалы времени, распределенные по экспоненциальному закону с параметром (i – число заявок в ИПВ в момент времени t ), и могут вновь попасть в конфликтные передачи. После успешной передачи заявка покидает систему.

Время обслуживания распределено по одному и тому же показательному закону с параметром , как для первичных, так и для повторных вызовов.

Будем считать, что на вход системы поступает простейший поток заявок с параметром . Структура такой СМО имеет вид рис. 1.1.

Состояние рассматриваемой системы определим вектором , изменение во времени которого образует однородный дискретный двумерный марковский процесс с бесконечным числом состояний.

Рис. 1.1 – Модель системы массового обслуживания

Математическая модель исследуемого протокола множественного доступа построена, проведем ее анализ, получим аналитические выражения, определяющие зависимости для основных ее характеристик.

Для исследования процесса введем следующие обозначения

,

вероятность того, что в момент времени t прибор находится в состоянии k и в ИПВ находится i заявок.

Рассмотрим вероятности переходов из состояния системы в произвольный момент времени t в состояние за бесконечно малый интервал времени .

1. Пусть система находится в состоянии , то есть в ИПВ находится i заявок и прибор свободен, за интервал времени состояние системы может измениться таким образом (рис. 1.2):

а) с вероятностью из входящего потока требований поступит новая заявка, которая немедленно займет прибор и начнет обслуживание, тогда система в момент времени будет находиться в состоянии ;

б) с вероятностью к прибору обратится одна из i заявок, находящихся в ИПВ и система перейдет в состояние ;

в) с вероятностью состояние системы не изменится.

2. Пусть система в момент времени t находится в состоянии , то есть прибор занят обслуживанием заявки и в ИПВ находится i требований, за интервал времени возможны следующие переходы (рис. 1.3):

а) с вероятностью прибор успешно завершит обслуживание, и в момент времени система будет находиться в состоянии ;

б) с вероятностью в систему поступит новое требование из входящего потока и произойдет конфликт. Как вновь поступившая, так и заявка с прибора перейдут в ИПВ, и начнется интервал оповещения о конфликте, следовательно, система перейдет в состояние ;

в) с вероятностью к прибору обратится одна из заявок с ИПВ, произойдет конфликт, и обе заявки переместятся в ИПВ, следовательно, система в момент времени будет находиться в состоянии ;

г) с вероятностью состояние системы не изменится.

3. Пусть система в момент времени t находится в состоянии . Посмотрим, что произойдет через интервал времени длины (рис. 1.4):

а) с вероятностью к прибору обратится заявка из входящего потока, которая автоматически попадет в ИПВ. В момент времени система будет в состоянии ;

б) с вероятностью интервал оповещения о конфликте завершится, и система перейдет в состояние ;

в) с вероятностью состояние системы не изменится.

Все остальные вероятности переходов не превышают порядка малости .

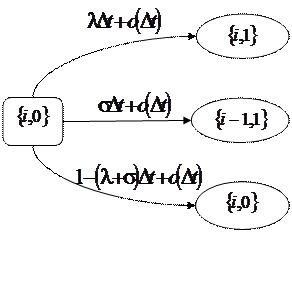Рис. 1.2 – Возможные переходы из состояния

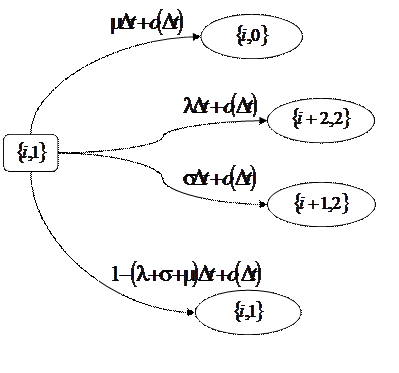Рис. 1.3 – Возможные переходы из состояния

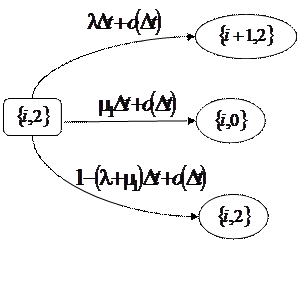Рис. 1.4 – Возможные переходы из состояния

Таким образом, можно записать систему конечно-разностных уравнений для вероятностей состояний системы: