Реферат: Асимптотические методы исследования нестационарных режимов в сетях случайного доступа

следовательно, в нестационарном режиме, эти вероятности удовлетворяют системе дифференциально-разностных уравнений

,

, (1.1)

,

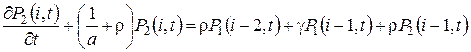где ,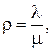

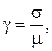
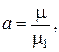
решить которую практически невозможно, но можно решить асимптотически в условиях «большой загрузки», т.е. при , , где пропускная способность исследуемой сети связи (верхняя граница множества тех значений загрузки , для которых в системе существует стационарный режим).

Рассмотрим исходную систему уравнений (1.1) и произведем в ней замену переменных: , , , . В результате замены производится переход от дискретной переменной к непрерывной переменной . В новых обозначениях производная равна .

Тогда систему (1.1) перепишем

,

, (1.2)

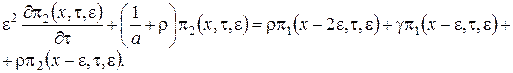
Получим вид решения системы (1.2), которую будем решать в три этапа.

1 этап. В уравнениях (1.2) устремим и обозначим , заметим что, . Будем иметь

,

, (1.3)

.

Выразим через 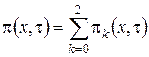и получим

,

, (1.4)

.

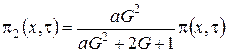где – асимптотическая плотность распределения вероятностей нормированного числа заявок в ИПВ.

Введем обозначения

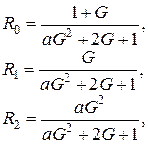(1.5)

( - это асимптотическая вероятность того, что обслуживающий прибор находится в состоянии k ). Из системы (1.3) следуют равенства, связывающие , , и выглядят так

(1.6)

.

Найдем вид функции . Для этого перейдем ко второму этапу.

2 этап . Неизвестные функции будем искать с точностью до в следующем виде

, (1.7)

Определим вид функций , для этого в системе уравнений (1.2) разложим функции с аргументом в ряд по приращению аргумента (ограничиваясь двумя слагаемыми), будем иметь

,

, (1.8)

В полученные уравнения подставим в форме (1.7), заменим разностью , сумму на G и не учтем слагаемые, имеющие порядок . Получим