Реферат: Асимптотические методы исследования нестационарных режимов в сетях случайного доступа
В уравнения (2.15) подставим ![]() в форме (2.14), приведем подобные и получим систему неоднородных линейных алгебраических уравнений относительно
в форме (2.14), приведем подобные и получим систему неоднородных линейных алгебраических уравнений относительно ![]() вида
вида
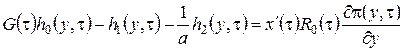 ,
,
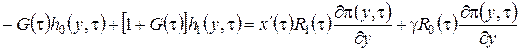 , (2.16)
, (2.16)
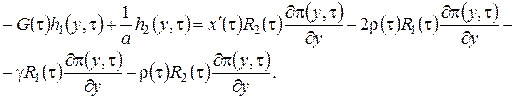
Нетрудно увидеть, что между уравнениями этой системы есть зависимость и ранг матрицы системы равен, следовательно, чтобы решение уравнений (2.16)существовало, необходимо выполнение равенства
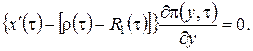 (2.17)
(2.17)
Из однородного линейного уравнения с частными производными первого порядка (2.9) мы знаем, что ![]() . Таким образом, можно сделать вывод, что система (2.16) разрешима. При условии, что функция
. Таким образом, можно сделать вывод, что система (2.16) разрешима. При условии, что функция ![]() известна, решение можно записать в виде
известна, решение можно записать в виде
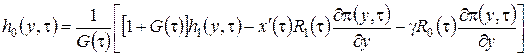 ,
,
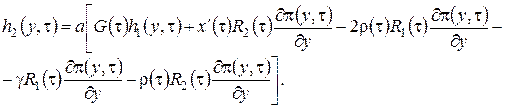 (2.18)
(2.18)
Теперь все готово, для того, чтобы найти функцию ![]() . Перейдем к третьему этапу.
. Перейдем к третьему этапу.
3 этап . В системе дифференциальных уравнений (2.11) все функции с аргументом ![]() разложим в ряд по приращению аргумента
разложим в ряд по приращению аргумента ![]() , ограничиваясь слагаемыми порядка
, ограничиваясь слагаемыми порядка