Реферат: АСУ двухстадийного дробления замкнутого цикла

Щековая дробилка является объек­том, работу которого характеризует производительность питателя Qп, ширина разгрузочной щели l, круп­ность D и прочность σ исходного мате­риала, а также производительность Qдр, мощность N, потребляемая в про­цессе дробления, и гранулометриче­ский состав дробленого продукта, ха­рактеризуемый средневзвешенным ди­аметром кусков d_ср .

Возможные отклонения ширины разгрузочной щели от заданного значения, как правило, своевременно уст­раняются обслуживающим персоналом

при профилактических осмотрах. Кро­ме того, изменение ширины разгрузочной щели в процессе эксплуатации на­столько мало, что его влиянием можно пренебречь.

С учетом сделанных ограничений: структурная схема щековой дробилки как объекта автоматического регулиро­вания производительности приведена на рис.4.1. в котором в качестве входного регулирующего воздействия рас­сматривается производительность пи­тателя Qп, в качестве выходной регу­лируемой величины -производитель­ность дробилки Qдр.

Рис 4.1. Структур­ная схема щековой дробилки как объекта автоматического ре­гулирования.

Приняв параметры механического режима щековой дробилки крупного дробления (угол захвата α, ход по­движной щеки S) неизменными, отне­сем к возмущающим воздействиям f изменение прочности σ и крупности D) исходного материала.

Уравнение материального баланса дробилки имеет вид

(4.1)

где Qп — производительность питате­ля; Qдp — производительность дробилки, или в операторной форме

(4.2)

где , , - изображе­ния Лапласа соответствующих величин.

Из уравнения (4.2) следует, что по каналу производительность питателя - запас материала в дробилке щековая дробилка является астатическим объектом. Дальнейшее исследование объекта связано с рассмотрением передаточной функции , характеризующих соответ­ственно взаимосвязь величин Qдр(s).

Производительность дробилки в пе­реходных режимах определяется не всем запасом материала, находящегося в текущий момент в дробилке, а некоторым эффективным количеством материала находящегося в непосредственном контакте с «призмой выпадения».

Исходя из этого объем материала можно представить в виде двух составляющих:

где - запас материала в зоне предварительного дробления; - запас материала в зоне эффективного дробления.

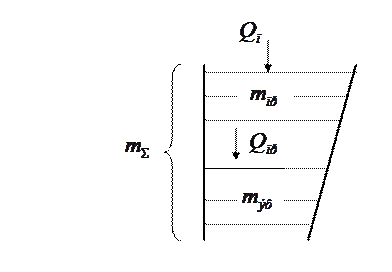
Рис. 4.2. Физическая модель процесса дробления в щековой дробилке

Физическая модель такого процесса дробления приведена на рис. 4.2.

Исходя из принципа разделения запаса материала на две зоны и применения к отдельным зонам выражения материального баланса (4.1), учитывая при этом функциональную зависимость между производительностью и полным запасом материала

составлена система дифференциальных уравнений, характеризующих динамику процессов, протекающих в щековой дробилке (запаздывание в объекте не учитывается).

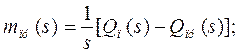
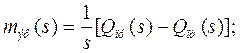
где Qпр — производительность в пред­варительной зоне дробления; - нелинейные функции, определяемые экспериментально.