Реферат: АСУ двухстадийного дробления замкнутого цикла

Из приведенной структурной схемы можно получить выражения передаточ­ных функций, связывающих

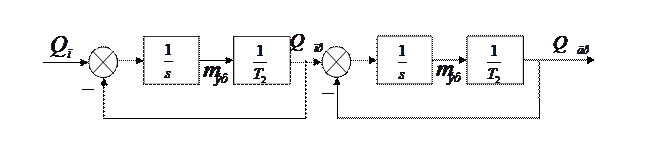
Рис. 4.3. Структурная схема щековой дро­билки

производительность дробилки с полным запасом материала m:

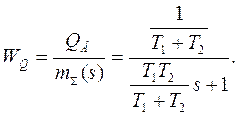
В разобранной структурной схеме щековой дробилки не учитывается чис­тое запаздывание, физическая приро­да которого связана с временем сво­бодного падения горной массы с пита­теля в камеру дробления τ1 и временем свободного падения дробленого мате­риала на конвейер, транспортирующий продукт, τ2. Однако это запаздывание необходимо учитывать. Пренебрегая изменением уровня материала на кон­вейере и запасом материала в камере дробления, можно принять τ1 и τ2 постоянными. С учетом выражений (4.3) и (4.4) можно записать:

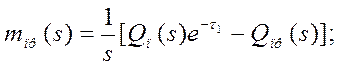(4.3)

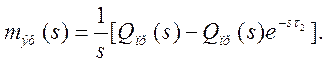(4.4)

Тогда передаточная функция по соответствующим каналам с учетом звеньев чистого запаздывания запишется так:

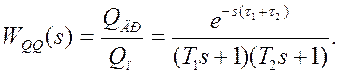
5. Расчет регулятора исследуемого объекта

Произведем расчет регулятора для системы, у которой производительность питателя на входе и дробилки на выходе. В качестве рассматриваемого объекта – щековая дробилка С-887, для которой

т/ч, =2.11 т, Т₁ =60 с, T₂ = 30 c, τ₁ = 2 c, τ₂ = 1 c.

Передаточная функция объекта равна

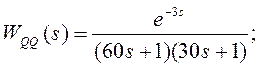
После разложения экспоненты в ряд Паде получим: =

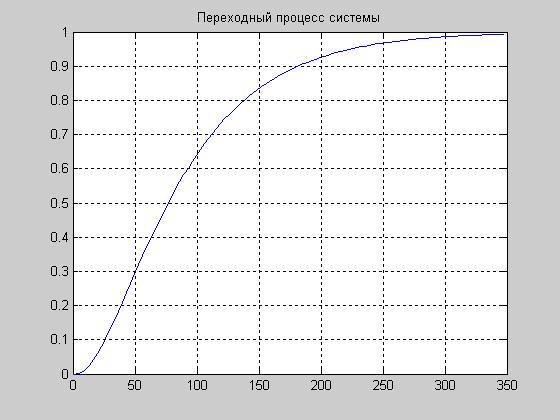
Рис. 5.1. Переходный процесс системы.

5.1 Расчет регулятора методом РЧХ

Согласно этому методу, расчетные формулы для настроек регулятора замкнутой системы, представленной на рис. 5.2, получают из условия, аналогичного критерию Найквиста.

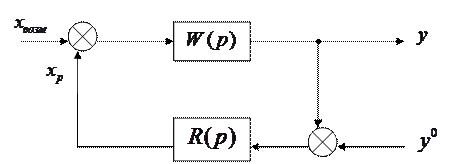Если разомкнутая система имеет степень колебательности не ниже заданной, то замкнутая систем будет обладать заданной степенью колебательности в том случае, когда расширенная КЧХ разомкнутой системы проходит через точку с координатами , т.е.

,

где (1)

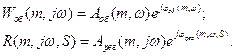
Уравнение (1) равносильно двум уравнениям, записанным относительно расширенных АЧХ и ФЧХ объекта и регулятора, а именно:

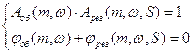(2)

Для заданных частотных характеристик объекта и выбранного закона регулирования при решении системы уравнений (2) находят вектор настроек регулятора S, обеспечивающих заданную степень колебательности на каждой частоте.

Самыми распространенными регуляторами являются П, ПИ и ПИД поэтому рассчитаем коэффициенты для данных регуляторов и выберем из них по переходному процессу наиболее оптимальный.

Формулы для расчета коэффициентов регуляторов получают из системы:

П: