Реферат: Автокорреляция и ее устранение

Можно показать, что аппроксимируется выражением .

Критерий Дарбина – Уотсона – метод обнаружения автокорреляции первого порядка с помощью статистики Дарбина – Уотсона.

Статистика критерия Дарбина – Уотсона вычисляется по формуле:

, где ek – остатки в наблюдениях авторегрессионной схемы первого порядка uk+1 = сuk + ee k+1.

Значение DW-статистики будем обозначать также через d.

Критерий Дарбина – Уотсона обнаруживает только ярко выраженную автокорреляцию первого порядка и лишь при отсутствии лаговых переменных в регрессии.

Если автокорреляция отсутствует, то p = 0, и поэтому величина d должна быть близкой к двум. При наличии положительной автокорреляции величина будет меньше двух; при отрицательной автокорреляции она будет превышать 2. Так как p должно находиться между значениями 1 и – 1, то d должно лежать между 0 и 4 [8, C.46].

Критическое значение d при любом данном уровне значимости зависит от числа объясняющих переменных в уравнении регрес­сии и от количества наблюдений в выборке. К сожалению, оно также зависит oт конкретных значений, принимаемых объясняющими переменными. Поэто­му невозможно составить таблицу с указанием точных критических значений для всех возможных выборок, как это можно сделать для t- и F-статистик; но можно вычислить верхнюю и нижнюю границы для критического значения d. Для положительной автокорреляции они обычно обозначаются как dU и dL.

На схеме 1.1 представлена данная ситуация. Стрелка указывает критический уровень d, который обозначается как dкрит. Если знать зна­чение dкрит, то можно сравнить с ним значение d, рассчитанное для регрессии. Если бы оказалось, что d dкрит, то невозможно было бы отклонить ну­левую гипотезу об отсутствии автокорреляции. В случае d dкрит возможно отклонить нулевую гипотезу и сделать вывод о наличии положительной автокор­реляции.

Схема 1.1 Тест Дарбина – Уотсона на автокорреляцию (положительная автокорреляция)

Вместе с тем знаем только, что dкрит находится где-то между dL и dU. Это предполагает наличие трех возможностей.

1. Величина d меньше, чем dL. В этом случае она будет также мень­ше, чем dкрит, и поэтому делаем вывод о наличии положитель­ной автокорреляции.

2. Величина d больше, чем dU. В этом случае она также больше кри­тического уровня, и поэтому невозможно отклонить нулевую гипо­тезу.

3. Величина d находится между dL и dU. В этом случае она может быть больше или меньше критического уровня. Поскольку нельзя опреде­лить, которая из двух возможностей налицо, невозможно ни отклон­ить, ни принять нулевую гипотезу.

В случаях 1 и 2 тест Дарбина—Уотсона дает определенный ответ, но случай 3 относится к зоне невозможности принятия решения, и изменить создавше­еся положение нельзя [6, C.18].

Таким образом, зона неопределенности критерия Дарбина – Уотсона – промежуток значений статистики Дарбина–Уотсона, при попадании в который критерий не дает определенного ответа о наличии или отсутствии автокорреляции первого порядка.

Проверка на отрицательную автокорреляцию проводится по аналогичной схеме, причем зона, содержащая критический уровень, расположена симмет­рично справа от 2. Так как отрицательная автокорреляция встречается относи­тельно редко, предполагается, что при необходимости самостоятельно вычисляются гра­ницы зоны на основе соответствующих значений для положительной автокор­реляции при данном числе наблюдений и объясняющих переменных. Как показано на Схеме 1.2 величина (4 - dU) есть нижний предел, ниже которого признается отсутствие автокорреляции, а (4 - dL) — верх­ний предел, выше которого делается вывод о наличии отрицательной автокор­реляции.

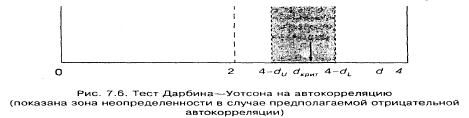
Схема 1.2 Тест Дарбина – Уотсона на автокорреляцию (отрицательная автокорреляция)

2 Поправка Прайса–Уинстена и метод Кохрейна–Оркатта устранения автокорреляции

Наилучший, но не всегда возможный, способ устранения автокорреляции – установление ответственного за нее фактора и включение соответствующей объясняющей переменной в регрессию.

В других случаях процедура, которую следует принять для устранения автокорреляции, будет зависеть от ха­рактера зависимости между значениями случайного члена. В литературе наиболь­шее внимание уделяется авторегрессионной схеме первого по­рядка uk+1= puk + ek+1, так как она интуитивно правдоподобна, но для того, чтобы было целесообразным ее использование в более сложных моделях, оснований обыч­но не хватает. Вместе с тем если наблюдения проводятся ежеквартально или ежемесячно, могут оказаться более подходящими другие модели.

Если бы уравнение uk+1= puk + ek+1 было правильной спецификацией для измерения величины случайного члена, то возможно было бы полностью устранить автокорре­ляцию, если бы знали величину p. Это будет продемонстрировано на примере уравнения регрессии, включающего только одну объясняющую переменную, од­нако при большем их числе действует тот же принцип [9, C.91].

Предположим, что истинная модель задается выражением ,

так что наблюдения t и t - 1 формируются как .

Теперь вычтем из обеих частей уравнения умноженное на p соотноше­ние и получим: .

Обозначим и .

Тогда формулу мож­но переписать как