Реферат: Баллистика и баллистическое движение
к этому углу, определяет tg ![]() и соответственно угол
и соответственно угол ![]() :
:
tg ![]() =
=![]() .
.
При равномерном движении по оси X проекция скорости движения v![]() остаётся неизменной и равной проекции начальной скорости v
остаётся неизменной и равной проекции начальной скорости v![]() :
:
v![]() = v
= v![]() cos
cos![]() .
.
Зависимость v![]() (t) определяется формулой:
(t) определяется формулой:
v![]() = v
= v![]() + a
+ a![]() t.
t.
в которую следует подставить:
v![]() = v
= v![]() sin
sin![]() , a
, a![]() = -g.
= -g.
Тогда
v![]() = v
= v![]() sin
sin![]() - gt.
- gt.
Графики зависимости проекций скорости ![]() от времени приведены на рис№2.
от времени приведены на рис№2.
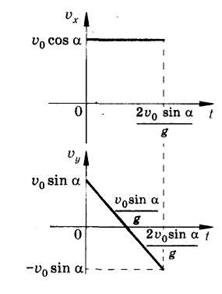 (рис №2).
(рис №2).
В любой точке траектории проекция скорости на ось X остается постоянной. По мере подъема снаряда проекция скорости на ось У уменьшается по линейному закону. При t = 0 она равна ![]() =
= ![]() sin а. Найдем промежуток времени, через который проекция этой скорости станет равна нулю:
sin а. Найдем промежуток времени, через который проекция этой скорости станет равна нулю:
0 = v![]() sin
sin![]() - gt , t =
- gt , t = ![]()
Полученный результат совпадает со временем подъема снаряда на максимальную высоту. В верхней точке траектории вертикальная компонента скорости равна нулю.
Следовательно, тело больше не поднимается. При t > ![]() проекция скорости
проекция скорости
v![]() становится отрицательной. Значит, эта составляющая скорости направлена противоположно оси Y, т. е. тело начинает падать вниз (рис.№3).
становится отрицательной. Значит, эта составляющая скорости направлена противоположно оси Y, т. е. тело начинает падать вниз (рис.№3).
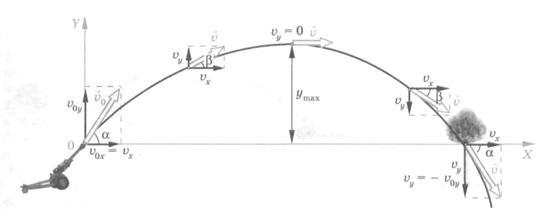 (рис№3)
(рис№3)
Так как в верхней точке траектории v = 0, то скорость снаряда равна:
v = v![]() = v
= v![]() cos
cos![]()
г) траектория движения тела в поле тяжести.
Рассмотрим основные параметры траектории снаряда, вылетающего с начальной скоростью v![]() из орудия, направленного под углом α к горизонту (рис №4).
из орудия, направленного под углом α к горизонту (рис №4).
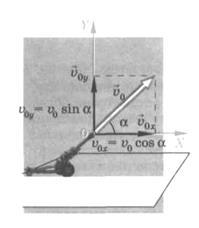 (рис №4)
(рис №4)
Движение снаряда происходит в вертикальной плоскости XY, содержащей v![]() .
.
Выберем начало отсчёта в точке вылета снаряда.
В евклидовом физическом пространстве перемещения тела по координатным
осям X и Y можно рассматривать независимо.
Ускорение свободного падения g направлено вертикально вниз, поэтому по оси X движение будет равномерным.
Это означает, что проекция скорости v![]() остаётся постоянной, равной её значению в начальный момент времени v
остаётся постоянной, равной её значению в начальный момент времени v![]() .
.