Реферат: Барицентрические координаты
Встречающееся ниже понятие «объединение нескольких материальных точек» можно наглядно истолковать как равнодействующую подводных весов всех тех шариков, которые наглядно изображают эти материальные точки.
Иногда полезно дать более широкое наглядное толкование понятия материальной точки с произвольной вещественной «массой».
|
рис. 5 |
Сделаем одно предварительное замечание. На каждой прямой мы можем выбрать положительное направление и единицу масштаба. Если это уже сделано, то прямую иногда называют осью .
Каждый отрезок (скажем, АВ ) можно рассматривать как направленный, причём сначала мы называем начало отрезка (А ), а затем — его конец (В ); направление отрезка — от А к В . Если отрезок лежит на оси (или параллелен ей), то его направление может:
1) совпадать с направлением оси;
2) быть противоположным направлением оси.
В первом случае мы величиной отрезка называем его длину; во втором случае величиной отрезка мы называем его длину, взятую со знаком минус (-).
Таким образом, величина отрезка , лежащего на какой-нибудь оси, или параллельного оси — это его длина, взятая со знаком плюс или минус, в зависимости от того, будут ли направление отрезка и оси одинаковы или противоположны. Величину отрезка АВ будем обозначать так: АВ .
В нашем примере (рис. 5) АВ =3, DC = -2, ВА = -3. Вообще АВ = -ВА .
Вернёмся теперь к вопросу о возможном физическом истолковании материальных точек с произвольными вещественными массами.
Мы будем представлять, что в пространстве произвольным образом выбрана какая-либо ось l . Материальную точку (А, т) можно наглядно истолковать как силу, параллельную оси l и приложенную к точке А .
Число т («масса») характеризует абсолютную величину (или, как говорят иногда, «напряжение») и направление этой силы: сила и ось одинаково направлены, если т >0, и противоположно направлены, если т <0; по абсолютной величине сила равна ½т ½ (единицам силы). Если т =0, то сила равна нулю. Материальную точку вида (А, 0) можно назвать «незагруженной точкой» или «нулевой силой».
|
С
рис. 6 |
Когда будем ниже говорить о «центре тяжести нескольких материальных точек», то его можно себе наглядно представлять как центр параллельных сил , а «объединение нескольких материальных точек» — как равнодействующую нескольких параллельных сил, приложенную в центре параллельных сил.
Для геометрических приложений важно, что почти всё основное, что мы говорили относительно материальных точек с положительными массами, возможно обобщить на случай материальных точек с произвольными вещественными массами.
Понятие центра тяжести двух материальных точек (с произвольными вещественными массами) можно ввести так.
Центром тяжести двух материальных точек (А, а) и (B, b ) (рис. 6) называется такая точка С , лежащая на оси АВ (положительное направление от А к В ), которая удовлетворяет условию: а × АС = b × СВ .
|
А
В С рис. 7 |
Центр тяжести С двух материальных точек (А, а) и ( B, b) будет лежать между А и В , лишь если «массы» а и b одного знака. Если а и b разных знаков, то С вне отрезка АВ (рис. 7).
Лишь в одном случае центр тяжести материальных точек (А, а) и ( B, b ) с различными носителями (А ¹ В ) не существует, — именно, когда массы их противоположны по знаку, но не равны по абсолютной величине (то есть, если а = -b ¹ 0 ). В связи с этим мы будем называть две материальные точки вида (А, а) и (В, -а) (А ¹ В , а ¹ 0 ) механической парой .
Этот случай можно себе представить как предельный для того случая, когда а ¹ - b , но а ® - b . Если а ¹ - b , а ¹ 0 , b ¹ 0 , то можно написать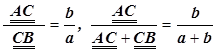 , т.е.
, т.е. 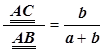 . Если а ® - b , то а + b ® 0 и, следовательно, АС ® ¥ , то есть точка С неограниченно удаляется вдоль прямой АВ . Поэтому иногда говорят, что если a = -b , то центр тяжести двух материальных точек (А, а) и (B, b) «лежит в бесконечно удалённой точке прямой АВ ».
. Если а ® - b , то а + b ® 0 и, следовательно, АС ® ¥ , то есть точка С неограниченно удаляется вдоль прямой АВ . Поэтому иногда говорят, что если a = -b , то центр тяжести двух материальных точек (А, а) и (B, b) «лежит в бесконечно удалённой точке прямой АВ ».
Оставаясь здесь в рамках элементарной геометрии, мы будем эту фразу рассматривать как образное выражение того, что центра тяжести в данном случае нет.
Если одна из двух материальных точек является незагруженной, а “масса” другой материальной точки отлична от нуля, то их центр тяжести совпадает с носителем загруженной точки. В связи с этим имеет смысл все незагруженные точки считать равными, то есть считать, что при любых А иВ ( А, 0) ºº (В, 0) .
 А
А