Реферат: Бескоалиционные игры

или

Преобразовав (3) и (4), получим

(1- x) y + (1- x) £ 0

(a11 - a12 - a21 + a22) xy + (a12 - a22) x ³ 0

или

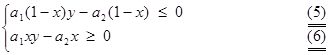
Т. о., множество всех приемлемых стратегий для игрока 1 удовлетворяет условиям (5) и (6), 0 £x£ 1; 0 £y£ 1. Чтобы найти x рассмотрим 3 случая :

1. Если x = 0, то (6) справедливо "y, а (5) имеет вид :

a1y-a2£ 0.

2. Если x = 1, то (5) справедливо "y, а (6) имеет вид :

a1y-a2³ 0.

3. Если 0 < x < 1, то (5) разделим на (1 -x), а (6) – на x и получим

Итак, множество К решений системы (5) – (6) состоит из

всех ситуаций вида (0; y), если a1y-a2£ 0; 0 £y£ 1;

всех ситуаций вида (x; y), если a1y-a2 = 0; 0 < x < 1;

всех ситуаций вида (1; y), если a1y-a2³ 0; 0 £y£ 1.

Если a1 = a2 = 0, то решением является xÎ[0; 1], yÎ[0; 1], т. к. все неравенства (7) – (8) выполняются при всех x и y, т. е. множество приемлемых для игрока 1 ситуаций покрывает весь единичный квадрат.

Если a1 = 0, a2¹ 0, то выполняется либо (7), либо (8), и поэтому решением является либо x = 0, либо x=1 при 0 £y£ 1 (приемлемой стратегии в игре не существует).

Если a1 > 0, то из (7) получаем решение

x = 0; y£:= a,

Из (8) следует ещё решение x = 1, y³a, из (9) следует ещё решение

0 < x < 1, y = a.

Если a1 < 0, то решение следующее :

x = 0, y ³a; x = 1, y £a; 0 < x < 1, y = a.

При этом необходимо учитывать, что дополнительно должно быть

0 £y£ 1.