Реферат: Быстрые вычисления с целыми числами и полиномами

предполагая, что n ₀ содержит (t + 1)двоичных цифр (т. е. что b_t ¹ 0 и b_{t + 1} = 0). В этих условиях вычисляемое выражение может быть записано:

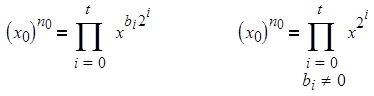или же .

Если задана последовательность (x_i )_{0 £ i £ t} , первый элемент которой есть x ₀ и x_i для i Î [1,t ] определено соотношением x_i = x_{i – 1} ² , то можно записать = P{x_i | 0 £i £t , b_i ¹ 0}. Чтобы завершить построение алгоритма и иметь возможность получить значение предыдущего произведения, необходимо вычислить биты b_i числа n ₀ . Для последовательности (n_i ) _{0 £ i £ t +1} (с начальным элементом n ₀ ), определённой соотношением n_i = [n_{i – 1} /2] для любого i Î [1, t + 1], бит b_i равен нулю, если n_i чётно, и равен единице в противном случае. Первое значение индекса i , для которого n_i равно нулю, есть t + 1.

Ясно, что число итераций, необходимых для выполнения алгоритма, зависит только от показателя n .

2^t £n £ 2^{t + 1} илиt £ log₂ n < t + 1.

Первая часть этого свойства может быть выражена следующим образом: [n /2^{t + 1} ] = 0 и [n /2^t ] ¹ 0, что позволяет точно определить число совершаемых делений n , равное числу итераций алгоритма при заданном значении n . Очевидно, нужно совершить t + 1 итераций, чтобы выполнить алгоритм, т. е. [log₂ n ] + 1 итераций. Следовательно, трудоёмкость алгоритма есть O (logn ).

Третий алгоритм – это классический алгоритм Евклида вычисления наибольшего общего делителя целых чисел. Мы предполагаем заданными два натуральных числа a и b и вычисляем их наибольший общий делитель (a ,b ).

2.3 Алгоритм Евклида

1. Вычислим r – остаток от деления числа a на b , a = bq +r , 0 £r < b .

2. Если r = 0, то b есть искомое число.

3. Если r ¹ 0, то заменим пару чисел (a ,b ) парой (b ,r ) и перейдём к шагу1.

Не останавливаясь на объяснении, почему алгоритм действительно находит (a ,b ), докажем некоторую оценку его сложности.

Теорема 1. При вычислении наибольшего общего делителя ( a , b ) с помощью алгоритма Евклида будет выполнено не более 5p операций деления с остатком, где p есть количество цифр в десятичной записи меньшего из чисел a и b .

Доказательство. Положим r ₀ = a > b и определим r ₁ ,r ₂ ,…,r_n - последовательность делителей, появляющихся в процессе выполнения шага 1 алгоритма Евклида. Тогда

r₁ = b ,…, 0£ r_i+1 < r_i , i = 0,1,…,n - 1.

Пусть также u ₀ = 1,u ₁ = 1,u_{k +1} = u_k + u_{k -1} ,k ³ 1, - последовательность Фибоначчи. Индукцией по i от i = n - 1 до i = 0 легко доказывается неравенство r_{i +1} ³u_{n - i} . А так как u_n ³ 10^{( n -1)/5} , то имеем неравенства 10^p > b = r ₁ ³u_n ³ 10^{( n -1)/5} и n < 5p +1.

Немного подправив алгоритм Евклида, можно достаточно быстро решать сравнения ax º 1 (modm ) при условии, что (a ,b ) = 1. Эта задача равносильна поиску целых решений уравнения ax + by = 1.

2.4 Алгоритм решения уравнения ax + by = 1

0. Определим матрицу E =

1. Вычислим r – остаток от деления числа a на b , a = bq + r , 0 £r < b .

2. Если r = 0, то второй столбец матрицы Е даёт вектор (x y ) решений уравнения.

3. Если r ¹ 0, то заменим матрицу Е матрицей

4. Заменим пару чисел (a ,b ) парой (b ,r ) и перейдём к шагу 1.

Если обозначить через Е _k матрицу Е , возникающую в процессе работы алгоритма перед шагом 2 после k делений с остатком (шаг 1), то в обозначениях из доказательства теоремы 1 в этот момент выполняется векторное равенство (a ,b )*E_k = (r_{k -1} ,r_k ). Его легко доказать индукцией по k . Поскольку числа a и b взаимно просты, имеем r_n = 1, и это доказывает, что алгоритм действительно даёт решение уравнения ax + by = 1. Буквой n мы обозначили количество делений с остатком, которое в точности такое же, как и в алгоритме Евклида.

Полиномиальные алгоритмы в теории чисел – большая редкость. Да и оценки сложности алгоритмов чаще всего опираются на какие-либо не доказанные, но правдоподобные гипотезы, обычно относящиеся к аналитической теории чисел.

Для некоторых задач эффективные алгоритмы вообще не известны. Иногда в таких случаях всё же можно предложить последовательность действий, которая, «если повезёт», быстро приводит к требуемому результату. Существует класс так называемых вероятностных алгоритмов, которые дают правильный результат, но имеют вероятностную оценку времени работы. Обычно работа этих алгоритмов зависит от одного или нескольких параметров. В худшем случае они работают достаточно долго. Но удачный выбор параметра определяет быстрое завершение работы. Такие алгоритмы, если множество «хороших» значений параметров велико, на практике работают достаточно эффективно, хотя и не имеют хороших оценок сложности.

3. Полиномиальная арифметика

Рассмотрим вероятностный алгоритм, позволяющий эффективно находить решения полиномиальных сравнений по простому модулю. Пусть p – простое число, которое предполагается большим, и f (x )ÎZ[x ] – многочлен, степень которого предполагается ограниченной. Задача состоит в отыскании решений сравнения

f (x ) º 0 (mod p ). (1)

Например, речь может идти о решении квадратичных сравнений, если степень многочлена f (x ) равна 2. Другими словами, мы должны отыскать в поле F_p = Z/p Z все элементы, удовлетворяющие уравнению f (x ) = 0.

Согласно малой теореме Ферма, все элементы поля F_p являются однократными корнями многочлена x^p - x . Поэтому, вычислив наибольший общий делитель d (x ) = (x^p - x , f (x )), мы найдём многочлен d (x ), множество корней которого в поле F_p совпадает с множеством корней многочлена f (x ), причём все эти корни однократны. Если окажется, что многочлен d (x ) имеет нулевую степень, т. е. лежит в поле F_p , это будет означать, что сравнение (1) не имеет решений.

Для вычисления многочлена d (x ) удобно сначала вычислить многочлен c (x )ºx^p (mod f (x )), пользуясь алгоритмом, подобным описанному выше алгоритму возведения в степень (напомним, что число p предполагается большим). А затем с помощью аналога алгоритма Евклида вычислить d (x ) = (c (x ) – x , f (x )). Всё это выполняется за полиномиальное количество арифметических операций.

Таким образом, обсуждая далее задачу нахождения решений сравнения (1) мы можем предполагать, что в кольце многочленов F_p [x ] справедливо равенство