Реферат: Быстрые вычисления с целыми числами и полиномами

1. Выберем каким-либо способом элемент d Î F_p .

2. Вычислим наибольший общий делитель

g (x ) = ( f (x ), (x + d )^(p-1)/2 – 1).

3. Если многочлен g (x ) окажется собственным делителем f (x ), то многочлен f (x ) распадается на два множителя и с каждым из них независимо нужно будет проделать все операции, предписываемые настоящим алгоритмом для многочлена f (x ).

4. Если окажется, что g (x ) = 1 или g (x ) = f (x ), следует перейти к шагу 1 и, выбрав новое значение d , продолжить выполнение алгоритма.

Количество операций на шаге 2 оценивается величиной O (lnp ), если вычисления проводить так, как это указывалось выше при нахождении d (x ). Выясним теперь, сколь долго придётся выбирать числа d , пока на шаге 2 не будет найден собственный делитель f (x ).

Количество решений уравнения (t + a ₁ )^{( p – 1)/2} = (t + a ₂ )^{( p – 1)/2} в поле F_p не превосходит (p -3)/2. Это означает, что подмножество D ÌF_p , состоящее из элементов d , удовлетворяющих условиям

(d + a₁ )^{(p – 1)/ 2} ¹ (d + a₂ )^{(p – 1)/ 2} , d ¹ -a₁ , d ¹ -a₂ ,

состоит не менее чем (p – 1)/2 из элементов. Учитывая теперь, что каждый ненулевой элемент b ÎF_p удовлетворяет одному из равенств b ^{( p – 1)/2} = 1, либо b ^{( p – 1)/2} = –1, заключаем, что для d ÎD одно из чисел a₁ , a₂ будет корнем многочлена (x + d ) ^{( p – 1)/2} – 1, а другое – нет. Для таких элементов d многочлен, определённый на шаге 2 алгоритма, будет собственным делителем многочлена f (x ).

Итак, существует не менее (p –1)/2 «удачных» выборов элемента d , при которых на шаге 2 алгоритма многочлен f (x ) распадается на два собственных множителя. Следовательно, при «случайном» выборе элемента d Î F_p , вероятность того, что многочлен не разложится на множители после k повторений шагов алгоритма 1-4, не превосходит 2^-k . Вероятность с ростом k убывает очень быстро. И действительно, на практике этот алгоритм работает достаточно эффективно.

Заметим, что при оценке вероятности мы использовали только два корня многочлена f (x ). При n > 2 эта вероятность, конечно, ещё меньше. Более тонкий анализ с использованием оценок А. Вейля для сумм характеров показывает, что вероятность для многочлена f (x ) не распасться на множители при однократном проходе шагов алгоритма 1-4 не превосходит 2^-n + O (p ^-1/2 ). Здесь постоянная в O (.) зависит от n . В настоящее время известно элементарное доказательство оценки А. Вейля.

Если в сравнении (1) заменить простой модуль p составным модулем m , то задача нахождения решений соответствующего сравнения становится намного более сложной. Известные алгоритмы её решения основаны на сведении сравнения к совокупности сравнений (1) по простым модулям – делителям m , и, следовательно, они требуют разложения числа m на простые сомножители, что, как уже указывалось, является достаточно трудоёмкой задачей.

3.2 Произведение и возведение в степень многочленов, заданных массивами

Условимся представлять многочлены массивами, индексированными, начиная с 0, в которых элемент с индексом i означает коэффициент многочлена степени i

type

Polynome =array [1..Nmax ] of Ring_Element ;

Следующий алгоритм даёт функцию умножения двух многочленов и , где многочлен степени (который даёт результат в конце алгоритма) должен быть предварительно инициализирован нулём.

for i := 0 to degP do

for j := 0 to degQ do

R [i +j ]:=R [i +j ]+P [i ]*Q [i ];

Изучая предыдущий алгоритм, устанавливаем, что его сложность как по числу перемножений, так и сложений, равна произведению высот двух многочленов: (degP + 1)(degQ + 1), но в этом алгоритме, который не учитывает случай нулевых коэффициентов, можно рассматривать высоту многочлена как число всех коэффициентов. Значит, возможно улучшить предыдущий алгоритм, исключив все ненужные перемножения:

for i := 0 to degP do

if P [i ] ¹ 0 then

for j := 0 to degQ do

if Q [j ] ¹ 0 then

R [i+j]:=R [i +j ]+P [i ]Q [i ];

Очень просто вычислить сложность алгоритма возведения в степень последовательными умножениями, если заметить, что когда P – многочлен степени d , то Pⁱ – многочлен степени id . Если обозначить C_mul (n ) сложность вычисления Pⁿ , то рекуррентное соотношение C_mul (i + 1) = C_mul (i ) + (d +1)(id +1) даёт нам:

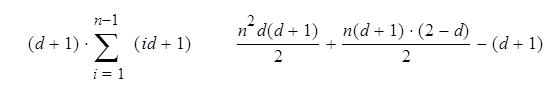C_mul (n ) = =

Что касается возведения в степень с помощью дихотомии (т.е. повторяющимися возведениями в квадрат), вычисления несколько сложнее: зная , вычисляем с мультипликативной сложностью. Как следствие имеем:

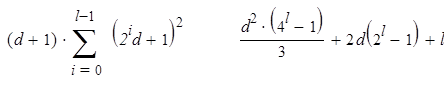C _sqr (2^l ) = = =
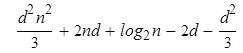