Реферат: Частотные критерии устойчивости

Введение

При формулировке алгебраических критериев и критерия Михайлова не имеет значения, какой системы (разомкнутой или замкнутой) исследуется устойчивость, т. е. рассмотренные критерии в равной мере применимы для исследования устойчивости разомкнутой и замкнутой систем.

Алгебраические критерии и критерий Михайлова применяются для исследования устойчивости и разомкнутой и замкнутой систем.

Разомкнутая система – это система, в которой отсутствует обратная связь между входом и выходом, т.е. управляемая величина (выходная) не контролируется.

Замкнутая система – это система регулирования по отклонению, на вход УУ через обратную связь поступает информация о фактическом изменении выходной величины.

Критерий Найквиста предназначен для исследования только замкнутых систем. Он позволяет по виду амплитудно-фазовой частотной характеристики разомкнутой системы судить об устойчивости замкнутой системы.

АФЧХ разомкнутой системы – это кривая, которую описывает конец вектора частотной передаточной функции разомкнутой системы в комплексной плоскости.

1. Частотные критерии устойчивости

Частотными критериями называются критерии устойчивости, основанные на, построении частотных характеристик и кривой Михайлова.

Будут рассмотрены следующие частотные критерии: критерий Михайлова, Найквиста и логарифмический частотный критерий.

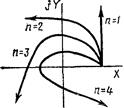
Рис.1 Схема для формулировки критерия Михайлова

Пусть характеристический полином системы равен:

Подставим в него :

Кривая Михайлова – это кривая, которую описывает конец вектора на комплексной плоскости при изменении от 0 до .

Критерий Михайлова. Для того чтобы система была устойчива, необходимо и достаточно, чтобы кривая Михайлова, начинаясь при с действительной положительной полуоси, при возрастании от 0 до последовательно обходила п квадрантов в положительном направлении, не попадая в начало координат (рис.1).

Пример Задан характеристический полином системы:

.

Оценить устойчивость системы по критерию Михайлова.

Сначала необходимо подставить в него , получим:

.

Для того, чтобы построить кривую Михайлова, представим характеристический полином в виде:

, т.е. ,

Для построения кривой составим таблицу:

	0	0<<1	1	1<<		>	®¥
	2	>0	1	>0	0	<0	® – ¥
	0	>0	0	<0	-1,4	<0	® – ¥

Построим кривую Михайлова (рис. 2, кривая 1). В пределах квадранта вид кривой Михайлова на устойчивость не влияет, и она строится весьма приблизительно. Система неустойчива.

Рис.2. Кривые Михайлова

При формулировке алгебраических критериев и критерия Михайлова не имеет значения, какой системы (разомкнутой или замкнутой) исследуется устойчивость, т. е. рассмотренные критерии в равной мере применимы для исследования устойчивости разомкнутой и замкнутой систем.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--