Реферат: Дефект масс и энергия связи ядер

Подставив в уравнения (3.1.5) и (3.1.6) радиус ядра r=r₀ A^1/3 , получим

(3 .1.7 )

(3.1.8)

а подставив (3.1.7) и (3.1.8) в (3.1.2), получим

. (3.1.9)

Постоянные α, β и γ подбирают такими, чтобы формула (3.1.9) лучшим образом удовлетворяла всем значениям энергий связи, вычисленным по экспериментальным данным.

Пятый член, представляющий парную энергию, зависит от четности числа нуклонов:

(3.1.10)

Ферми уточнил также постоянные по новым экспериментальным данным. Полуэмпирическая формула Бете-Вейцзекера, выражающая массу нуклида в старых единицах (¹⁶ О=16 ), получилась такой:

M(A, Z) = 0,99391A – 0,00085 + 0,014A2/3 + +0,083(A/2 – Z)2 A-1 + 0,000627Z2 A-1/3 + π0,036A-3/4

(3 .1.11 )

Для четных нуклидов π = –1; для нуклидов с нечетным А π = 0; для нечетных нуклидов π = +1.

К сожалению, эта формула весьма устарела: расхождения с действительными величинами масс может достигать даже 20 Мэв и имеет среднее значение около 10 Мэв.

В многочисленных дальнейших работах первоначально лишь уточняли коэффициенты или вводили некоторые не слишком важные дополнительные члены. Метрополис и Рейтвизнер еще раз уточнили формулу Бете–Вейцзекера:

M(A, Z) = 1,01464A + 0,014A2/3 + +0,041905 + π0,036A-3/4

(3.1.12)

Для четных нуклидов π = –1; для нуклидов с нечетным А π = 0; для нечетных нуклидов π = +1.

Вапстра предложил учитывать влияние оболочек с помощью члена такого вида:

(3.1.13)

где A_i , Z_i и W_i – эмпирические постоянные, подбираемые по опытным данным для каждой оболочки.

Грин и Эдварс ввели в формулу масс следующий член, характеризующий влияние оболочек:

(3.1.14)

где α _i , α _j и K_ij – постоянные, полученные из опыта; и – средние значения N и Z в данном интервале между заполненными оболочками.

п.3.2. Новые полуэмпирические формулы с учетом влияния оболочек

Камерон исходил из формулы Бете—Вейцзекера и со­хранил два первых члена формулы (3.1.9). Член, выражающий поверхностную энергию E_S (3.1.7), был изменен.

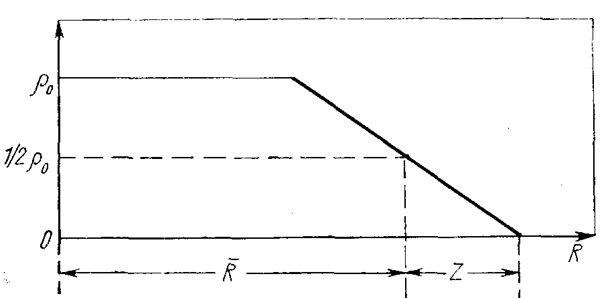
Рис. 3.2.1. Распределение плотности ядерной мате­рии ρ по Камерону в зависимости от расстоя­ния до центра ядра. А —средний радиус ядра; Z — половина толщины поверхностного слоя ядра.

При рассмотрении рассеяния элек­тронов на ядрах, можно сделать вывод, что распределение плотности ядерной материи в ядре ρ _n трапециеобразно (рис. 16). За средний радиус ядра т можно принять расстояние от центра до точки, где плотность убывает вдвое (см. рис. 3.2.1). В результате обработки опытов Хофштедтера. Камерон предложил такую формулу для среднего радиуса ядер:

Он считает, что поверхностная энергия ядра пропорциональна квадрату среднего радиуса r² , и вводит поправку, предложен­ную Финбергом, учитывающую симметрию ядра. По Каме­рону, поверхностную энергию можно выразить так:

?????????, ???????????, ???? ??????? (3.1.9) ????? ??? ????????? ? ????? ? ??????????????? ?????????????? ?????????? ????. ????????? ??? ???????????? ????? ????? ???
????? ????. ??????? ???? ????? ??????????? ???????? ????, ??????????????? ?????????? ? ???????? ???????? ? ???? ? ????? ??????????? ????????? ????????. ???????? ????

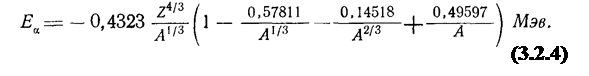Таким образом, избыток масс, по Камерону, выразится так:

М - А = 8,367А - 0,783Z + αА +β+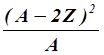

+ Е _S + E_C + Е_α = П (Z, N). ( 3 .2.5)

Подставив экспериментальные значения М—А методом наи­меньших квадратов получили следующие наиболее надежные значения эмпирических коэффициентов (в Мэв):

α=–17,0354; β=– 31,4506; γ=25,8357; φ=44,2355. (3.2.5а)

С помощью этих коэффициентов были вычислены массы. Рас­хождения между вычисленными и экспериментальными массами показаны на рис. 3.2.2. Как можно заметить, в некоторых случаях расхождения достигают 8 Мэв. Особенно велики они у нукли-дов с замкнутыми оболочками.

Камерон ввел дополнительные слагаемые: член, учитываю­щий влияние ядерных оболочек S(Z, N), и член P(Z, N) , харак­теризующий парную энергию и учитывающий изменение массы в зависимости от четности N и Z :

М—А=П( Z , N)+S(Z, N)+P(Z, N). (3.2.6)