Реферат: Дискретные сигналы
Обработка сигналов на цифровых ЭВМ начинается с замены непрерывного сигнала X(t) на дискретную последовательность, для которой применяются такие обозначения
x(nT) , x(n) , xn , {x0 ; x1 ; x2 ; … } .
Дискретизация осуществляется электронным ключом (ЭК) через равные интервалы времени T (Рис. 1.1).
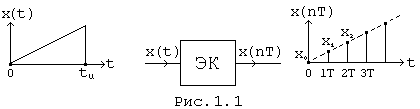
Дискретная последовательность аппроксимирует исходный сигнал X(t) в виде решетчатой функции X(nT). Частота переключения электронного ключа fд и шаг дискретизации T связаны формулой
fд = 1 / T . (1.1)
Дискретная последовательность или дискретный сигнал выражается через исходный непрерывный (аналоговый) сигнал следующим образом
x(nT) = x(t)![]() d(t - nT) , (1.2)
d(t - nT) , (1.2)
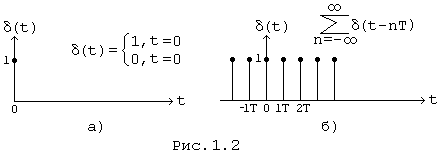
где d(t) - дискретная d - функция (Рис. 1.2, а),
![]() d(t - nT) - последовательность d - функций (Рис. 1.2, б).
d(t - nT) - последовательность d - функций (Рис. 1.2, б).
Погрешность, возникающую при замене аналогового сигнала дискретным сигналом, удобно оценить сравнивая спектры этих сигналов.
Связь спектров дискретного и непрерывного сигналов.
Исходное выражение для спектра дискретного сигнала с учетом (1.2) запишется следующим образом
X(jw) =![]() x(nT) e-j w t dt =
x(nT) e-j w t dt =![]() x(t)
x(t)![]() d(t - nT) e-j w t dt .
d(t - nT) e-j w t dt .
Периодическую последовательность d - функций здесь можно разложить в ряд Фурье
![]() d(t - nT) =
d(t - nT) =![]() ,
,
где с учетом формулы связи спектров периодического и непериодического сигналов
![]() , поскольку Fd (jw) = 1
, поскольку Fd (jw) = 1
После замены в исходном выражении периодической последовательности d - функций ее разложением в ряд Фурье получим
X(jw) =![]() x(t)(
x(t)(![]() ) e-j w t dt =
) e-j w t dt =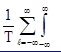 x(t)
x(t)![]() e-j w t dt .
e-j w t dt .
Учитывая здесь теорему смещения спектров, т.е. :
если f(t) ® F(jw), то f(t)![]() ® F[j(w±w0 )] ,
® F[j(w±w0 )] ,
последнее равенство можно представить в виде формулы, выражающей связь спектров дискретного X(jw) и аналогового Xa (jw) сигналов
X(jw) =![]() Xa [j(w -
Xa [j(w -![]() )] . (1.3)
)] . (1.3)
На основании формулы (1.3) с учетом поясняющих рисунков 1.3, а, б можно сделать следующие выводы :

Спектр дискретного сигнала состоит из суммы спектров исходного непрерывного сигнала, сдвинутых друг относительно друга по оси частот на величину равную частоте дискретизации wд
Спектры аналогового и дискретного сигналов совпадают в диапазоне частот [-0,5wд ; 0,5wд ], если удовлетворяется неравенство
wв Ј 0,5wд , (1.4)
--> ЧИТАТЬ ПОЛНОСТЬЮ <--