Реферат: Доверительный интервал. Проверка статистических гипотез
Функция потерь – дискретная случайная величина С, которая каждому из событий АВ, 
В, А
, ставит в соответствие потери 
, выраженные в каких-то единицах. Правильному решению естественно положить нулевые потери, а ошибкам первого и второго ряда положить соответственно положительные потери (числа) С1 и С2 , которые нужно задать.
Пусть ро = р(АВ или ), р1 = р(В), р2 = р(А). Определение значений этих вероятностей будет проведено ниже. Ряд распределения для случайной величины С имеет вид
| С | 0 | с1 | с2 |
| р | ро | р1 | р2 |
Определение. Математическое ожидание М(С) случайной величины С называется функцией риска и обозначается буквой r.
Таким образом, r = М(С) = 0 ро + с1 р1 + с2 р2 = с1 р1 + с2 р2 .
Введение функции риска приводит к естественному выбору решающего правила. Из двух правил лучшим считается то, которое приводит к меньшему риску. Для нахождения минимума функции риска найдем вероятности р1 и р2 :
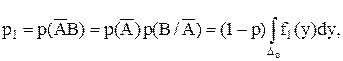
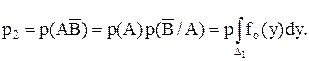
Тогда
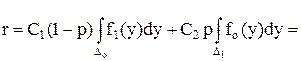
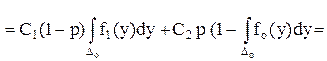
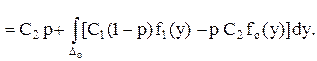
Для того, чтобы интеграл был минимальным, а значит и минимальное значение принимала функция риска r, нужно в состав Dо включить только те у, в которых подыинтегральная функция
С1 (1-р) f1 (y) – pC2 fo (y) < 0,
а в состав D1 - остальные значения у.
Последнее неравенство можно записать в виде
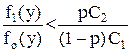
Функция f1 (y)/fo (y) называется отношением правдоподобия.
Итак, оптимальное решающее правило заключается в следующем: полученное в результате эксперимента значение у подставляется в отношение правдоподобия f1 (y)/fo (y) и сравнивается с числом
l =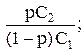 
если полученное в результате вычисления число f1 (y)/fo (y) меньше l, принимается гипотеза Но ; в противном случае – гипотеза Н1 .
Величина l носит название порога, а оптимальное решающее правило носит название порогового критерия оптимальности.