Реферат: Двухзеркальная антенна по схеме Кассергена

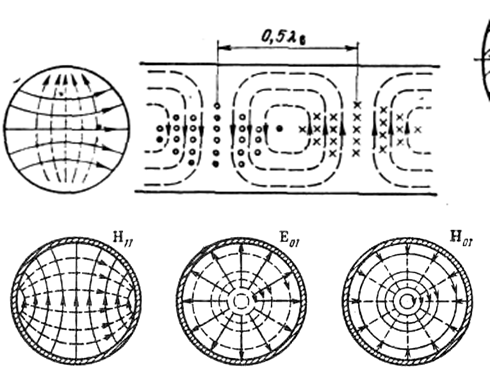Рис. 2.5.Структура поля H ₁₁ в круглом волноводе

Рис. 2.5. Структура поля H₁₁ в круглом волноводе:(———— линии элек-трического поля; — — — линии магнитного поля.

Электромагнитная волна типа E _mn ( H_mn ) распостраняется по волноводу, если ыполняется условие (2.18.).

Критическая длина волны для волн типа H_mn определяется из соотношения:

(2.25.)

где ‑ h _{m n} – «n »-ый корень производной функции Бесселя «m»-го –порядка.

Для волн типа E _mn :

(2.26.)

где ‑x _mn – «n »-ый корень функции Бесселя «m »-го порядка.

Расчитаем критические длины волн для волн, которые могут распостраняться на частоте 11 ГГц в выбранном круглом волноводе.

Для основной волны H ₁₁ :

29,298 мм.

Для волны E ₀₁

22,88 мм.

Для волны H ₂₁ :

17,95 мм.

Для волны H ₀₁ :

14,34 мм.

Волны E ₀₁ , H ₂₁ , H ₀₁ , на зданной частоте распосграняться не будут, так как не выполняется условие (2.18).

Примерный вид конструкции спользуемого для согласования плавного перехода от прямоугольного волновода к круглому изображён на рис. 2.6 . и в приложении 4.

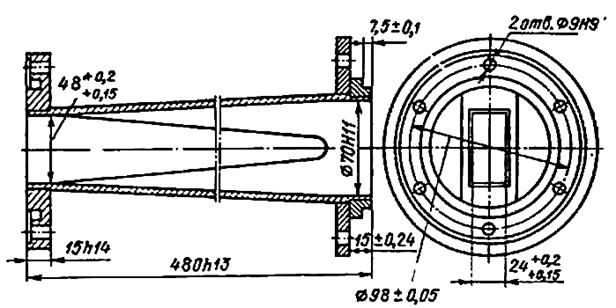Рис. 2.6. Конструкция плавного перехода с прямоугольного волновода с сечением 48´24 мм. на круглый диаметром 70 мм.

3. электрические характеристики антенны.

3.1. диаграмма направленности облучателя.

??? ???? ?????????? ?????, ? ???????? ?????????? ?????????? ??????? ??? ?????? ?????????? ??????????????? ???????? (?? ????????? ?? ???. 2.4., ?????? ? ?????? ???? ????????? ?????????? ??????? ????? ??????????????? ??????? ? ?????? ????? ???????????? (??? ?????? ???????), ? ????? ???? q = j ₀ , ??? j ₀ ? ???? ?????? ?? ???? ?????? ??????????).

рис. 2.4.

Диаграмма направленности диэлектрической антенны изображённой на рис. 2.4. может быть рассчитана по приближённой формуле:

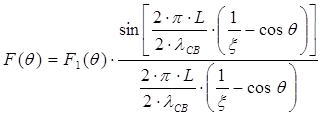(2.27.)

Где угол q отсчитывается от оси диэлектрического стержня, а также:

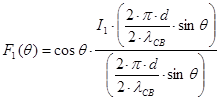‑ в плоскости (2.28.)

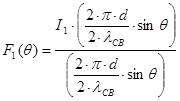‑ в плоскости (2.29.)

Ширину главного лепестка диаграммы направленности по уровню половинной мощности приближённо можно рассчитать по формуле:

= 22,72° (2.30.)

Расчётные формулы взяты из [1] на с. 10

Диаграмма направленности диэлектрической антенны должна получиться такой, чтобы нули главного лепестка приходились на такой угол q , что нулевое излучение диэлектрической антенны приходилось на края гиперболоида.

Рассчитанная диаграмма направленности изображена в приложении 1.

3.2. поле в раскрыве рефлекторов.

Наиболее просто направленные свойства параболической антенны рассчитываются так называемым апертурным методом, т.е. по полю в её раскрыве.

При установке в фокусе главного рефлектора облучателя с диаграммой направленности F_ОБЛ (y,a) в раскрыве зеркала наводится синфазное поле с амплитудным распределением и это амплитудное распределение поля можно рассчитать воспользовавшись формулой из [1] на с. 23, которая учитывает, что облучателем параболоида является гиперболоид:

(2.31.)

При этом координаты точек раскрыва x_p , y_p , f_p , a _p связаны с углами y и a соотношениями, обусловленными геометрией задачи (смотрите рис. 2.5. ):

(2.32.)

(2.33.)

(2.34.)

(2.35.)

Рассчитанное по этим формулам амплитудное распределение поля в раскрыве рефлекторов изображено в приложении 2.

3.3 диаграмма направленности и коэффициент усиления всей антенны.

По известному полю в раскрыве рефлекторов рассчитывается F( q, j) по формуле:

(3.1.)

Где:

(3.2.);

S ‑ поверхность раскрыва;

S_T – площадь проекции на раскрыв затеняющих элементов.

Коэффициент усиления антенны с учётом апертурного коэффициента исполизования gа (или КИП), обусловленного амплитудной неравномерностью поля в раскрыве, и коэффициента перехвата мощности облучателя зеркалом g_п рассчитывается по формуле:

(3.3.)

Где:

(3.4.)