Реферат: Ефект Ганна

Перевірив: ст.викладач

Б.О. Полежаєв

“___”___________ 2004 p.

Дніпропетровськ 2004

Зміст

стр.

1. Реферат …………………………………………………………………....3

2. Вступ …………………………………………………………….………...4

3. Ефект Ганна …………………………………………………….…….…... 5

4. Діод Ганна, генератори Ганна …………………………….….…………14

5. Висновок ………………………………………………………….……... 20

6. Список використаної літератури ………………………………………..21

1. Реферат

Дана робота містить 21 сторінку та складається з 6 розділів: вступу, рефератної частини, теоретичної сторони ефекту Ганна, практичної сторони – діодів та генераторів Ганна, висновку та списку використаної літератури. Також має 14 ілюстрацій (10 рисунків: 4 ескпериментальних графіки, 3 зображення реальних діодів, 7 схематичних зображення) і 10 розрахункових формул.

Діоди Ганна, генератори Ганна, N – подібна ВАХ, негативний опір, арсенид галію, фосфит індію, домен, Дж. Ганн, зонна енергетична структура з двома мінімумами, пікова характеристика I =I (t ).

2. Вступ

У даній роботі розглядаються процеси, що проходять у однорідних напівпровідниках електронного типу провідності при сильних електричних полях. Цей ефект спостерігається в арсеніді галія, фосфиту індію та інших напівпровідниках, де існує два мінімума в енергетичній структурі кристалу. Виникнення негативної частини графіку ВАХ відбувається у результаті різних значень рухливості електронів у двох мнімумах цих матеріалів. На основі цього явища можна конструювати генератори, які можуть працювати на високих частотах від 1 до 50 ГГц , при цьому частота визначається довжиною кристалу. У зв’язку з підвищенною увагою до спектру надвисоких частот електромагнітних хвиль в останні роки, можна сказати, що вивчення цих явищ є досить актуальним.

3. Ефект Ганна

Виникнення негативної диференційної провідності в однорідних напівпровідниках під дією сильного електричного поля.

У сильних електричних полях рухливість носіїв заряду починає залежати від напруженості прикладеного поля: µ = µ (ε). Внаслідок цього статична провідність напівпровідника σ₀ = enµ , що входить у дифиринційний закон Ома (i = enµ ε = σ₀ ε), зберігаючись позитивною, може істотно змінити своє значення із зміною напруженості поля. Залежно від характеру цієї зміни, диференціальна провідність напівпровідника

може виявитися як величиною позитивною, так і негативною.

Перший випадок реалізується тоді, коли із ростом напруженості поля ε рухливість носіїв µ збільшується, так що або зменшується настільки слабко, що хоча , але абсолютне значення 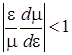, внаслідок чого вираз 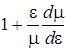, зберігає позитивний знак.

Другий випадок реалізується тоді, коли з ростом ε рухливість носіїв заряду µ падає, причому настільки різко, виконується не тільки умова , але й 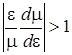. Тоді вираз 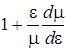, стає негативним, що й приводить до значення меншим за нуль.

У напівпровідниках, зона провідності яких має більше одного мінімуму енергії, електрон з хвильовим вектором k , що відповідає одному з мінімумів, при розсіюванні може виявитися у стані із хвильовим вектором k ' , що належить іншому мінімуму. У результаті такого розсіювання буде мати місце перекидання електронів з одного мінімуму в інший мінімум зони провідності. Такий вид розсіювання одержав назву «міждолинного».

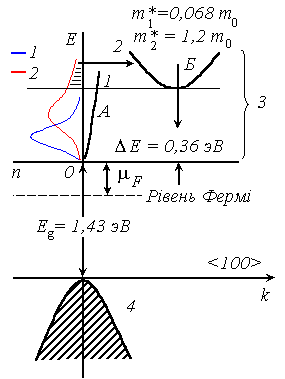Міждолинне розсіювання носіїв заряду у певних умовах може приводити до виникнення коливань струму із частотою порядку 10¹⁰ Гц при прикладенні до однорідного напівпровідника сильного постійного електричного поля. Це явище, назване ефектом Ганна , уперше спостерігалось на СаАs .

На рис. 3.1 зображена енергетична структура арсеніду галію у напрямку осі <100> . Істотним тут є наявність двох мінімумів А и Б , розділених зазором ΔE =0,36 еВ , в яких ефективні маси електронів різні. В області нижчої долини А електрони легкі, з ефективною масою m *=0,068m ₀ , вони мають високу рухливість [μ₁ ≈ 4000 ч 8000 см ² /(В · с )]. В області високої долини Б електрони важкі з m * = 1,2m ₀ і мають низьку рухливість [μ₁ ≈ 100 см ² /(В · с )]. Щільність станів у верхній долині приблизно в 1500 разів вище, ніж у нижній долині. Під час відсутності зовнішнього поля електрони, що перейшли з донорних рівнів у зону провідності, перебувають у термодинамічній рівновазі із граткою напівпровідника, маючи однакову з ним температуру T ₀ . Вони можуть займати енергетичні рівні як у нижньому, так і у верхньому мінімумах зони. Відповідні концентрації в їхніх мінімумах становлять:

та ,

де - відстань від дна зони провідності (нижнього рівня) до рівня Фермі (рис. 3.1).

Маємо відношення

.

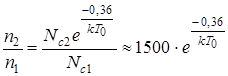Для T ₀ = 300K маємо:

k ₀ = 0,026 еВ і .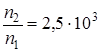

Оскільки енергія електронів значно менше енергетичного зазору kТ << ΔЕ , тоді електрони в основному будуть займати енергетичні рівні в нижчій долині зони провідності (~99,8 %) (рис. 3.3, а), де вони мають високу рухливість, малу ефективну масу й малу щільність станів. На рис. 3.1 показана крива розподілу Больцмана електронів зони провідності по енергіях при T ₀ =300K (крива 1). Вона практично не простирається в область енергій, що відповідає верхньому мінімуму.

Розглянемо тепер, який вплив на характер розподілу електронів по енергіях може зробити сильне поле. Електричне поле, змушуючи дрейфувати електрони, передає їм енергію. У результаті розсіювання електронів ця енергія переходить в енергію їх хаотичного теплового руху — електронний газ «розігрівається». У сильному полі його температура Т_е може значно перевищувати температуру гратки T ₀ . Відповідно до цього підвищується енергія електронів і крива їхнього розподілу по енергіях, деформуючись, простирається в область високих енергій (рис. 3.1, крива 2). Це приводить до появи все більшого числа електронів, здатних переходити з нижнього мінімуму у верхній (рис. 3.3 б). На рис. 3.1 область кривої розподілу, що відповідає заповненню верхнього мінімуму, заштрихована, а самі переходи електронів з мінімуму в мінімум показані горизонтальною стрілкою.

Розрахунок показує, що для арсеніду галію

,

причому починаючи з поля ε ≈ 3∙ 10⁵ В /м коефіцієнт γ > 1. Тому у полях з напруженістю ε >3∙ 10⁵ В /м температура електронного газу починає різко збільшуватися з ростом εі вже при ε≈ 3,5∙ 10⁵ В /м досягає значення T _е ≈ 600К . При такій температурі електронного газу відношенняn ₂ /n ₁ ≈ 1,75. Це означає, що при ε ≈ 3,5∙ 10⁵ В /м більша частина електронів зони провідності з’являється не у нижньому, а у верхньому мінімумі. (рис. 3.3 в) тому що рухливість електронів у верхньому мінімумі значно менше (в 40 разів), аніж у нижньому, тоді перехід великої кількості електронів з нижнього мінімуму у верхній повинен супроводжуватися різким зменшенням їхньої ефективної рухливості, а отже, і зменшенням густини струму, що протікає через напівпровідник, яке у цьому випадку описується наступною формулою:

j = e (n ₁ µ₁ + n ₂ µ₂ ) ε.

На рис. 3.2 прямій ОD показана залежність j ₁ =j ₁ (ε), накреслена в припущенні, що всі електрони зони провідності перебувають у нижньому мінімумі (п ₁ = п; n ₂ = 0), маючи рухливість µ₁ . Ця пряма нахилена до осі абсцис під кутом α_1. На цьому ж рисунку наведена пряма ОС , щовиражає залежність j ₂ =j ₂ (ε)у припущенні, що всі електрони перебувають у верхньому мінімумі (п ₁ = 0; n ₂ = n ), маючи рухливість µ₁ . Пряма нахилена до осі абсцис під кутом α₂ < α_1.

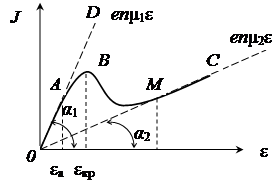Простежимо тепер, як міняється щільність струму в напівпровіднику в міру збільшення напруженості поля ε. Доти поки ε виявляється недостатнім, щоб викликати істотний розігрів електронів, всі вони залишаються в нижньому мінімумі й залежністьj =j (ε) описується прямою ОD. Однак у міру росту εвсе більше число електронів здобуває енергію, необхідну для переходу з нижнього мінімуму у верхній. Тому що цей перехід супроводжується падінням рухливості електронів, то він приводить до зменшення густини струму. Однак у міру росту εвсе більше число електронів здобуває енергію, достатню переходу з нижнього мінімуму 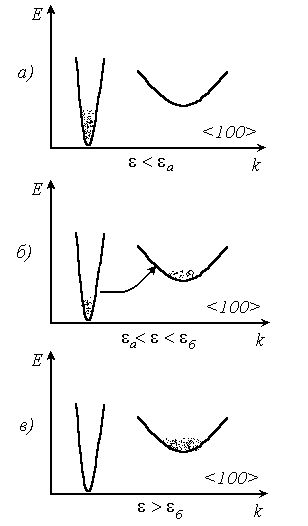у верхній. Тому що цей перехід супроводжується падінням рухливості електронів, то він приводить до зменшення густини струму. Тому починаючи з деякої напруженостіε₁ наростання струму j зростом εспочатку сповільнюється, а при ε = ε_а повністю зупиняється. При подальшому збільшенні εперехід електронів у верхній мінімум протікає настільки інтенсивно, що j не тільки не зберігається постійним, а падає з ростом ε(ділянка ВМ). Відповідно до цього диференціальна провідність напівпровідника на цій ділянці виявляється величиною негативної: < 0. Падіння j з ростом εтриває до напруженості ε_б , при якій переважна більшість електронів переходить у верхній мінімум. Після цього залежність j =j (ε) знову здобуває лінійний характер з кутом нахилу прямій j =j (ε),рівним α_2.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--