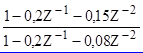Реферат: Эффекты конечной разрядности и их учет

где - дисперсия шума на выходе i-го источника шума. Учитывая характер шума, дисперсия шума на выходе источника будет определяться известными формулами:

- при округлении чисел

- при усечении чисел (4.4)

Следовательно, при округлении чисел

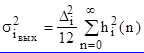
Дисперсия шума от всех источников на выходе цепи, при условии отсутствия корреляции между источниками шума, определяется суммой дисперсий шума от всех источников

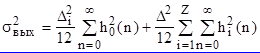(4.5)

где - дисперсия шума на выходе АЦП при округлении чисел.

- дисперсия шума на выходе каждого из Z множителей при округлении чисел.

Вероятностная оценка шума характеризует усредненный уровень энергии шума, поэтому в реальных условиях не исключены кратковременные скачки помехи относительно расчетного значения.

Влияние структуры ЦФ на шум квантования

Уровень шума квантования зависит от добротности полюсов передаточной функции. Добротность К-ого полюса определяется по формуле

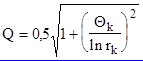(4.6)

где r_k - радиус полюса, Z_k = (Рис. 4.2, а), Q_к = w_к Т - угол полюса, w_к - частота полюса.

Действительно, поскольку Z = e^pT , то

следовательно

Отсюда

поэтому

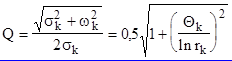
Чем выше добротность полюсов, тем выше уровень шумов квантования поскольку высокой добротности соответствует длительная циркуляция сигнала по цепи ОС при условии медленного снижения уровня сигнала с каждым новым обходом петли обратной связи. Но цепь ОС содержит, как правило, умножители, поэтому с каждой новой циркуляцией по цепи ОС сигнал все больше поражается помехой.

Реализация цепи на каскадном принципе позволяет ослабить негативное воздействие полюсов на помехозащищенность сигнала если, с одной стороны, каждому полюсу подобрать в пару ближайший к нему нуль (при совпадении полюса и нуля влияния полюса на шум полностью исключено), с другой стороны - располагать звенья в порядке нарастания добротности полюсов.

Основой каскадной реализации является представление передаточной функции в виде произведения простейших сомножителей в числителе и знаменателе

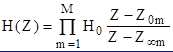(4.7)

где Z_0m - нули H(Z), Z_{Ґ m} - полюсы H(Z).

Сомножителям 1-го порядка (нули и полюсы - вещественные) соответствуют звенья 1-го порядка, сомножителям 2-го порядка (нули и полюсы - комплексно-сопряженные) соответствуют звенья 2-го порядка. При этом добротность вещественных полюсов тем выше, чем ближе к единичной окружности на плоскости Z располагается полюс.

Пример. Построить цепь на каскадном принципе по известной передаточной функции

H(Z) = 0,8