Реферат: Економіко-математичне моделювання процесу ціноутворення на ринку опціонів

Як і в інших моделях припускається, що на ринку обертаються акції з ціновим процесом {X_t , t ≥0}, який підпорядковується рівнянню

dX_t = μX _t dt + σX _t dW_t (1)

де {W_t , t ≥0} − стандартний броунівський рух; μ , σ = const ,μ − коефіцієнт росту, σ − коефіцієнт волатильності ціни базового активу. Припускається, що Х ₀ >0 і за акціями не виплачуються ніякі дивіденди при 0 ≤ t ≤ T .

Замість того щоб припускати обіг на ринку безризикових облігацій, автором припускається, що у банку в момент укладання угоди можна отримати довільну кількість кредитів на суму B ₀ >0 кожний під безризикову ставку r , що неперервно нараховується і є сталою величиною. Позичену суму разом з нарахованими відсотками необхідно повернути наприкінці дії опціонного контракту. Обсяг кредитного боргу B_t в момент часу t становить B ₀ e^rt .

У відповідності з цією корекцією припускається, що в момент часу t =0 укладається опціонний контракт європейського типу на купівлю однієї акції з ціною реалізації К та строком дії Т ; при цьому покупцем опціону виплачується премія С ₀ , що становить вартість опціону в початковий момент часу. Продавець опціону бере β ₀ кредитів на суму B ₀ кожний і інвестує отримані за кредитом кошти і премію за опціоном в γ ₀ акцій. Таким чином, в початковий момент часу формується портфель π ₀ = (β ₀ , γ ₀ ), такий, що його вартість становить Π₀ = γ ₀ X ₀ − β ₀ B ₀ і дорівнює С ₀ . Перед продавцем опціону постають два питання: якою має бути премія С ₀ ; якої стратегії хеджування слід дотримуватись при торгівлі цінними паперами, тобто якими мають бути коефіцієнти β _t і γ _t в кожний момент часу дії опціонного контракту, щоб вартість портфеля π _t , сформованого на основі цієї премії та з цими траекторіями коефіцієнтів хеджування, в момент часу Т дорівнювала виплатам по опціону, тобто Π_T ≡ γ _T X_T - β _T B_T = max{0, x − K }.

На підставі запропонованих автором припущень та з урахуванням обмежень на ціну опціонну отримана модель, яка співпадає з моделлю Блека-Шоулза:

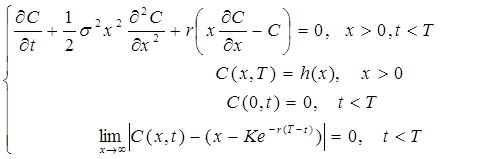(2)

Її точний розв’язок має вигляд:

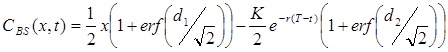(3)

де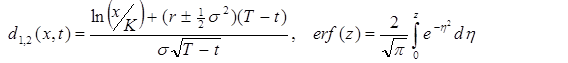

Проте структура хедж-портфелю у відповідності із зробленою корекцією змінюється таким чином: в кожний момент часу t необхідно тримати портфель, у якому буде β (Х_t ,t ) кредитів та γ ₍ Х_t , t ) акцій, де Х_t − ціна акції в момент часу t , і функції β та γ визначаються за формулами:

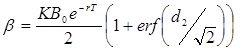(4)

Легкість та ефективність застосування на практиці результатів, отриманих Ф. Блеком та М. Шоулзом, обумовило появу на ринку програмної торгівлі, тобто торгівлі деривативами, хеджування яких відбувається за допомогою формування портфелю із структурою, що розраховується за формулами, аналогічними формулам (4).

Аналіз особливостей ведення програмної торгівлі показує, що існують деякі проблеми, які не враховані в класичній моделі Блека-Шоулза - проблема операційних витрат та наявності ефекту зворотнього зв’язку. Перша проблема пов’язана з тим, що при реалізації стратегій хеджування, тобто при динамічній зміні кількості базового активу у хедж-портфелі, продавець опціону має певні операційні витрати (маржа, комісійні, податки). На основі аналізу характеру їх оплати зроблено висновок, що найбільш впливовими є комісійні, які сплачуються посередникам за операції купівлі-продажу базового активу на ринку і становлять певний відсоток від суми транзакції. З урахуванням умови сплати комісійних у розмірі λ відсотків, автором отримано наступну модель визначення ціни опціону:

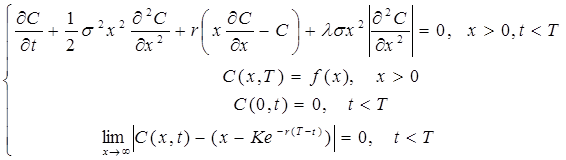(5)

та знайдено її точний розв’язок:

(6)

тобто

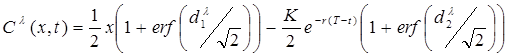(7)

де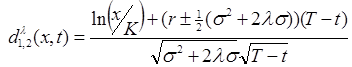

Відповідні стратегії хеджування обчислюються за формулами, аналогічними формулам (4).

Проведене в роботі дослідження характеру впливу операційних витрат на вартість опціону дозволило зробити наступні висновки. Було з’ясовано, що при відсутності операційних витрат, тобто при λ = 0, ціна опціону може розраховуватись за формулою Блека-Шоулза (3). Врахування майбутніх операційних витрат призводить до збільшення початкової премії за опціон і, як наслідок, зростає ціна опціону в кожний момент часу. Чим більшими є операційні витрати, тим більшою є ціна опціону.

Також досліджувалось питання, настільки суттєвим є вплив операційних виплат на ціну опціону. Це питання зводиться до оцінки функції Δ (x ,t ) =C ^λ (x ,t ) −C_BS (x ,t ) та характеру її залежності від параметрів. Максимальне значення по t функція Δ (x ,t ) набуває при t =0 при будь-яких фіксованих значеннях параметрів T , K , r , σ , λ :

max{Δ (x ,t ), t Î [0, Т] }=Δ (x ,0)

Тому замість оцінки функції Δ (x ,t ) оцінювалась функція δ^λ (x ): =Δ (x ,0).

В результаті автором були встановлені, математично доведені і економічно обґрунтовані наступні закономірності:

Зростання волатильності базового активу σ спричиняє збільшення впливу операційних витрат на ціну опціону, тобто

для будь-яких фіксованих значень Т , K , r , λ .