Реферат: Экспертные оценки в управлении

в которой число строк соответствует числу объектов, а число столбцов числу экспертов. Поскольку оценки важности одного и того же объекта, полученные от разных экспертов, могут не совпадать (числа в строках, вообще говоря, различны), то возникает задача определения показателей важности , представляющих собой усредненное мнение всех экспертов.

Определение значений по матрице можно осуществить, выбирая в качестве меры близости между и элементами соответствующей строки среднеквадратическую

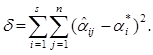(6.2)

Величины выбираются таким образом, чтобы среднее квадратическое отклонение было минимальным. При этом необходимо обеспечить, чтобы удовлетворяли условию нормировки:

.

В результате усредненные показатели важности рассчитываются по формулам вида

(6.3)

Таким образом, относительные оценки важности объектов вычисляются как среднеарифметические оценок, выставленных всеми экспертами. Отметим, что полученный результат является простейшим и применяется в тех случаях, когда ЛПР уверено в одинаковой компетентности и объективности экспертов.

Если у ЛПР нет уверенности в равном уровне компетентности экспертов, то применяется более сложная процедура обработки экспертных оценок. Вводятся коэффициенты компетентности экспертов , отвечающие условиям

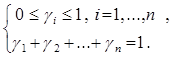(6.4)

При этом формула (6.3) обобщается и принимает вид:

(6.5)

Представим последнее равенство в матричной форме. Для этого введем векторы-столбцы

где верхний символ обозначает операцию транспонирования. В результате формула (6.5) примет следующий вид:

(6.6)

сли компетентность экспертов известна, то расчет усредненных оценок важности следует производить по формулам (6.5) или (6.6). Очевидно, в случае одинаковой компетентности экспертов

формула (6.5) сводится к (6.3).

Более сложным (и реалистическим) является случай, когда коэффициенты компетентности неизвестны и подлежат определению. Обычно в этом случае используется рекуррентный метод расчета с использованием матрицы экспертных оценок , который мы кратко опишем ниже.

Обозначим через вектор коэффициентов компетентности на - м шаге вычислений . Примем, что на первом шаге

Для - го шага оказываются справедливыми соотношения

(6.7)

, (6.8)

где - нормирующий множитель, вычисляемый из условия:

Подставляя (6.7) в (6.8) получим более удобное для использования соотношение:

, (6.9)

где квадратная симметрическая матрица называется матрицей взаимосвязи экспертных оценок и определяется равенством: