Реферат: Электрические и плазменные явления в атмосфере
![]() .
.
В области головки клин переходит в закругление. Пространственное распространение зарядов в лавине в два последовательных момента времени показано на рисунке.

Ассоциации сферических аэрозолей в газе и плазме. При диффузии аэрозолей в воздухе наступает такой момент, когда их поверхности соприкасаются. Тогда за счет взаимодействия, а также за счет химических процессов на поверхности, аэрозоли не слипаются, т.е. происходит их ассоциация. Пусть радиус одного сорта аэрозолей равняется ![]() , радиус второго
, радиус второго ![]() . В начале рассмотрим случай, когда один аэрозоль первого сорта покоится, так что на его поверхность приходит диффузионный поток аэрозолей второго сорта. Полный ток аэрозолей на расстоянии r от центра пробного аэрозоля равняется
. В начале рассмотрим случай, когда один аэрозоль первого сорта покоится, так что на его поверхность приходит диффузионный поток аэрозолей второго сорта. Полный ток аэрозолей на расстоянии r от центра пробного аэрозоля равняется ![]() , где D – коэффициент диффузии аэрозолей второго типа
, где D – коэффициент диффузии аэрозолей второго типа ![]() - их плотность. Так как аэрозоли не поглощаются в объеме, то и ток не зависит от расстояния r , т.е. i = const:
- их плотность. Так как аэрозоли не поглощаются в объеме, то и ток не зависит от расстояния r , т.е. i = const:
![]() , где
, где ![]() - плотность аэрозолей второго типа вдали от поглощающего центра при
- плотность аэрозолей второго типа вдали от поглощающего центра при ![]() проходит ассоциация аэрозолей, т.е.
проходит ассоциация аэрозолей, т.е. ![]() от
от ![]() .
. ![]() . Уравнение баланса для ассоциационных аэрозолей имеет вид:
. Уравнение баланса для ассоциационных аэрозолей имеет вид:
![]() ,
,
где ![]() - плотность аэрозолей первого типа,
- плотность аэрозолей первого типа, ![]() - константа скорости ассоциации, которая равна
- константа скорости ассоциации, которая равна ![]() .
.
При диффузном характере движения каждого из аэрозолей для среднего квадрата относительного расстояния между аэрозолями имеем
![]()
![]() .
.
Если r много больше ![]() - длина свободного пробега, тогда сила сопротивления аэрозоли будет определяться функцией стокса и при движении аэрозолей радиус
- длина свободного пробега, тогда сила сопротивления аэрозоли будет определяться функцией стокса и при движении аэрозолей радиус ![]() со скоростью
со скоростью ![]()
![]() , где
, где ![]() - вязкость воздуха. Придадим аэрозолю заряд e , тогда подвижность
- вязкость воздуха. Придадим аэрозолю заряд e , тогда подвижность ![]() , где t – температура воздуха
, где t – температура воздуха ![]()
![]() , где E – напряженность электрического поля
, где E – напряженность электрического поля ![]() (3). Вводя число Клудсена
(3). Вводя число Клудсена ![]()
![]() . Для воздуха при атмосферном давлении температуре равной 300К эта формула имеет вид
. Для воздуха при атмосферном давлении температуре равной 300К эта формула имеет вид 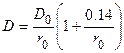 ,
, ![]()
![]()
![]() из (3) в (2)
из (3) в (2) ![]() . Для воздуха при температуре t =300K
. Для воздуха при температуре t =300K![]() . k не зависит от сорта аэрозолей.
. k не зависит от сорта аэрозолей.
Рассмотрим теперь заряженные аэрозоли. Пусть 1-![]() , 2-
, 2-![]() . При расстоянии r между ними сила их взаимодействия равна
. При расстоянии r между ними сила их взаимодействия равна ![]() . Эта сила уравновешена с силой Стокса, так что + аэрозоли движутся на встречу – заряду со скоростью
. Эта сила уравновешена с силой Стокса, так что + аэрозоли движутся на встречу – заряду со скоростью 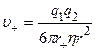 , где
, где ![]() - радиус положительной аэрозоли.
- радиус положительной аэрозоли.
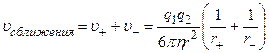 .
.
За пробный возьмем положительный аэрозоль и проведем вокруг него сферу радиуса r . Частота ассоциаций для рассматриваемого положительного аэрозоля есть произведение площади выбранной сферы на поток отрицательно заряженных частиц, пересекает ее 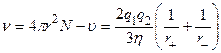 . Введем константу скорости ассоциации заряженной аэрозоли в соответствии с уравнением баланса
. Введем константу скорости ассоциации заряженной аэрозоли в соответствии с уравнением баланса
![]()
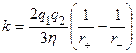 (7)
(7)
Сравнив (6) и (7) => диффузионный механизм существен для аэрозолей больших размеров: ![]() . В этом случае энергия кулоновского взаимодействия двух аэрозолей при соприкосновении << их тепловой энергии.
. В этом случае энергия кулоновского взаимодействия двух аэрозолей при соприкосновении << их тепловой энергии.
Рассмотрим ассоциационный аэрозоль во внешнем электрическом поле. Электрическое поле наводит на аэрозоль дополнительные моменты, а взаимодействие этих дипольных моментов при некоторых их пространственных конфигурациях отвечает притяжение частиц. В этом случае взаимодействие приводит к сближению и ассоциации аэрозолей.
Потенциал взаимодействия двух частиц с дипольной молекулой ![]() и
и ![]() .
.
![]() ,
,
где r – расстояние между частицами, n – единичный вектор вдоль направления соединения частиц.
Поскольку в рассматриваемом случае дипольные моменты аэрозолей наводятся внешним полем, то ![]() (
(![]() - компонента тензора поляризуемости аэрозолей в направлении электрического поля
- компонента тензора поляризуемости аэрозолей в направлении электрического поля ![]() ). В соответствии с условием задачи, направление E и D совпадают. Тогда
). В соответствии с условием задачи, направление E и D совпадают. Тогда 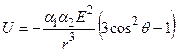 ,
, ![]() - угол между направлениями соединений аэрозолей (0<
- угол между направлениями соединений аэрозолей (0<![]() <
<![]() - притяжение).
- притяжение).
Для силы, действующей на взаимодействие аэрозолей при больших расстояниях между ними запишем
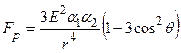 ;
;
![]() ;
; ![]()
![]() изменяется меньше
изменяется меньше ![]() и в области притяжения стремится его уменьшить, тем самым
и в области притяжения стремится его уменьшить, тем самым ![]() у3скоряет ассоциацию аэрозолей. При
у3скоряет ассоциацию аэрозолей. При ![]() =0, когда притяжение аэрозолей максимально,
=0, когда притяжение аэрозолей максимально, ![]() =0, т.е., при которой ассоциация проходит наиболее эффективно,
=0, т.е., при которой ассоциация проходит наиболее эффективно, ![]() не существенно, т.е. ею можно пренебречь
не существенно, т.е. ею можно пренебречь
 ;
;
 ;
;
 выделяем элементарный объем V вблизи проб. аэрозоли. Поверхность V обеспечивает одинаковое значение t ассоциационной аэрозоли.
выделяем элементарный объем V вблизи проб. аэрозоли. Поверхность V обеспечивает одинаковое значение t ассоциационной аэрозоли.  ,
, ![]() , где
, где ![]() - расстояние до поверхности при
- расстояние до поверхности при ![]() =0.
=0.