Реферат: Электронные цепи СВЧ (конспект) Add1
Параметры матрицы рассеяния могут быть рассчитаны по известной матрице проводимости четырехполюсника по формуле:
,
где 
– единичная матрица.
Необходимо отметить важную особенность параметров матрицы рассеяния, связанную с направлением прохождения сигнала. При изменении направления передачи изменятся лишь индексы в параметрах рассеяния (
на 
, 
на 
), знаки же величин, входящих в уравнения (3.1) останутся прежними.
Установим связь между параметрами волновой теории (S -матрицей) и параметрами классической теории (Y -матрицей). Для этого рассмотрим четырехполюсники с направлениями падающих и отраженных волн, а также токов и напряжений, как показано на рисунках, и, соответствующие данным системам параметров, уравнения:
Рис. 3.2 Четырехполюсники в системе волновой и классической теорий
 |  |
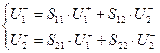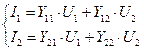Учитывая введенные ранее обозначения для падающих и отраженных волн
,
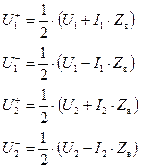а также выразив из этих уравнений токи и напряжения, подставим их в уравнения для S -параметров:
.
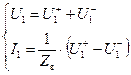
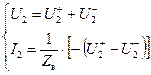(минус, так как ток 
направлен из четырехполюсника).
Рис. 3.3 К расчету S-матрицы по матрице Y
Подставляя в уравнения для 
параметров, получим:
.
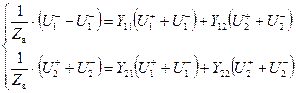Приведем к общему знаменателю:
.
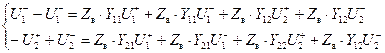Перегруппируем слагаемые
.
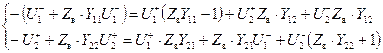и выразим из полученных уравнений падающие и отраженные волны:
.
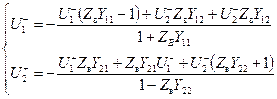Далее учтем нормировку матрицы проводимости: 
.
.
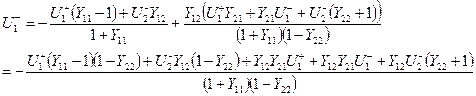Первое уравнение получим в виде:
.
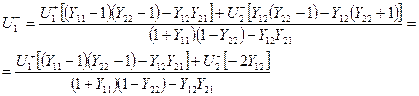Преобразуем второе уравнение:
.
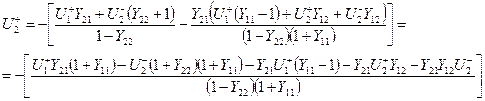Получим:
Матрица коэффициентов полученной системы запишется:
.
Волновая матрица передачи . Если в качестве зависимых переменных выбрать волны на входе четырехполюсника – волну падающую на вход и волну отраженную от входа, а в качестве независимых переменных – волны на выходе - распространяющуюся к нагрузке и отраженную от нагрузки, то система уравнений, коэффициентами в которой будут параметры волновой матрицы передачи, запишется:
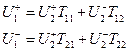
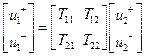. (3.2)
Описание четырехполюсников в виде волновой матрицы передачи удобно при их каскадном соединении. Результирующая матрица передачи в этом случае определится по соотношению:
.
Где k -количество каскадно соединенных четырехполюсников.
Можно показать, что для взаимных четырехполюсников справедливо соотношение 
, а для симметричных: 
.
--> ЧИТАТЬ ПОЛНОСТЬЮ <--