Реферат: Элементарная теория сумм Гаусса
D1 (t1 – t1 ) = D2 (t2 – t2 ) (mod D2 ) А так как D2 (t2 – t2 ) = 0 (mod D2 )
То по свойству сравнений имеем D1 (t1 – t1 ) = 0 (mod D2 ) Отсюда так как (D1 , D2 )=1 , то t1 – t1 = 0 (mod D2 ) Аналогично получим t2 – t2 = 0 (mod D1 )
Т.е. имеем t1 = t1 (mod D2 ) и t2 = t2 (mod D1 ) . Но это противоречит тому, что t1 пробегает полную систему вычетов по модулю D2 , а t2 пробегает полную систему вычетов по модулю D2 , так как в полной системе вычетов любые два числа не сравнимы. Следовательно наше предположение было неверным и действительно D1 t1 + D2 t2 пробегает полную систему вычетов по модулю D1 D2 .
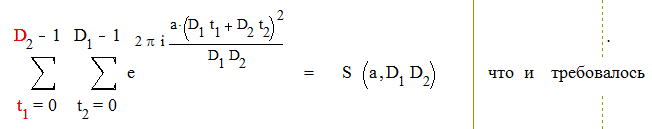 |
Поэтому
Лемма 3.
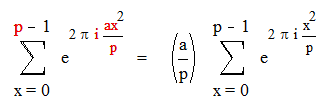 |
Пусть p простое нечетное число и не делит a . Тогда
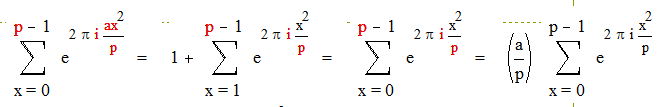 |
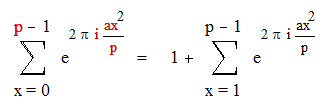 |
Доказательство:
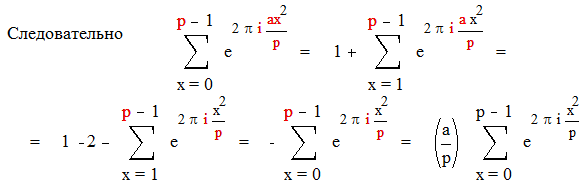 |
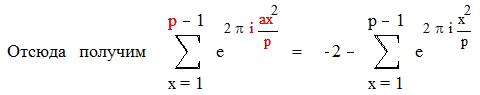 |
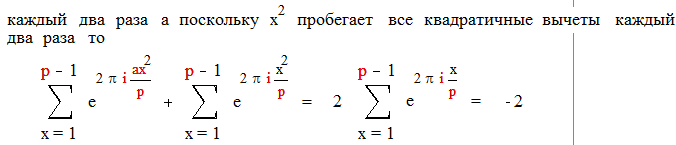 |
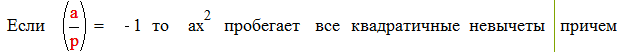 |
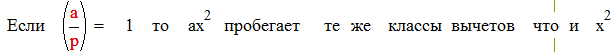 |
что и требовалось доказать.
-6-
Лемма 4.
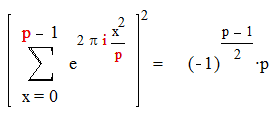 |
Если р простое нечетное число , то
Доказательство :
Из леммы 3. получим
 |
Так как произведение сопряженных величин дает квадрат модуля, то
 |
Лемма 5.
Если р и q различные простые числа , то
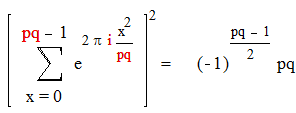 |
Доказательство :
Так как ( р, q )= 1 , мы можем воспользоваться леммой 2 : в нашем случае
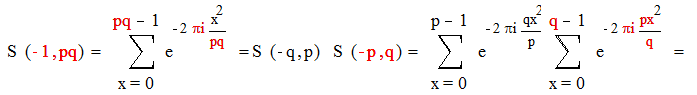 |
 |
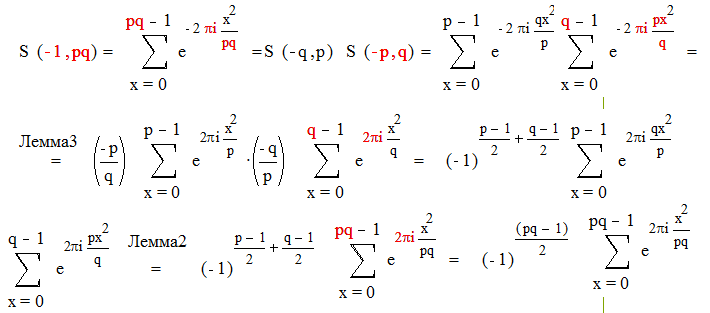 |
Итак , мы показали, что
 |
что и требовалось доказать.