Реферат: Элементарная теория сумм Гаусса

Рассмотрим следующую сумму – сумму Гаусса :

где D – целое положительное и (a, D)= 1.

Покажем, что значение суммы будет одним и тем же, если х пробегает любую полную систему вычетов по модулю D.

Действительно, пусть х пробегает полную систему вычетов по модулю D. Тогда х=qD+k , где k =0, 1, …, D-1 , q є Z

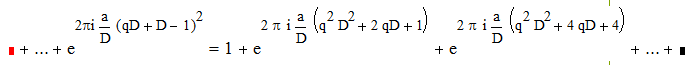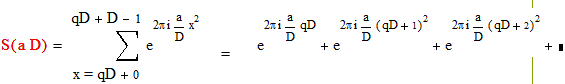Будем иметь :

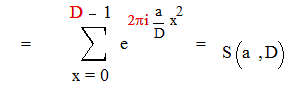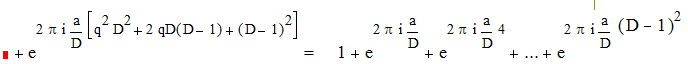что и требовалось.

Лемма 1.

Пусть (a, D)=1. Тогда:

Доказательство:

По свойству модуля комплексного числа :

Имеем:

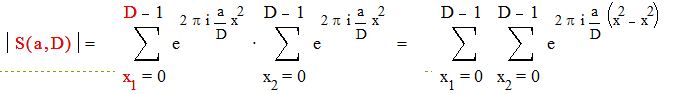Сделаем замену x = x + t . Когда х и х пробегают полную систему вычетов по модулю D , от х и t пробегают независимо полные системы вычетов по модулю D.

Действительно, пусть х и х пробегают полную систему вычетов по модулю D . Тогда х = qD + k k=0, 1, …, D-1 , q є Z

х = pD + i i=0, 1, …, D-1 , p є Z

Следовательно, t = x – x = (q – p)D + (k – i) = l D + m , где m=0, 1, …, D-1 , l є Z

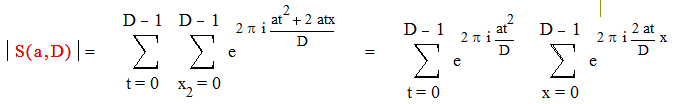а) Пусть D – нечетное, т.е. (2а, D)=1

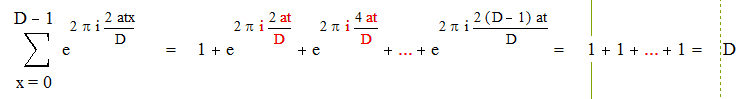если D делит t.

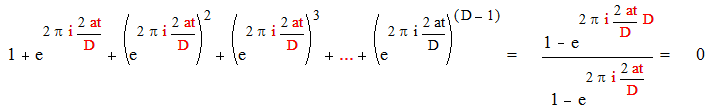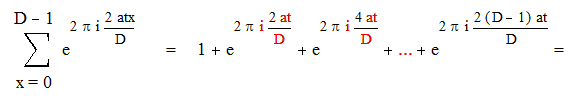Если же D не делит t, то последнюю сумму можно записать в виде :

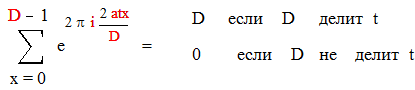Получили :

Тогда

Отсюда

б) Пусть D делится на 4, т.е. возможно представление : D = 2D , где D – четное и ( a, D )=1 .

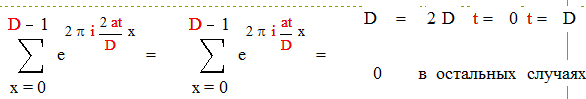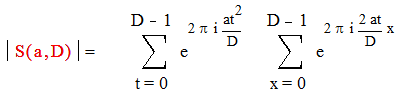Получим :

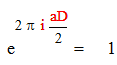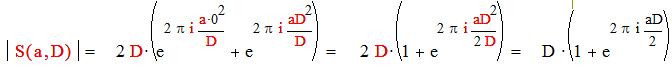Так как D четное, то

Следовательно

в) Пусть D = 2 (mod 4) , т.е. D = 4q + 2 , q є Z

Тогда из предыдущего случая имеем : D = 2 (2q+1)= 2D , D - нечетное. Имеем :

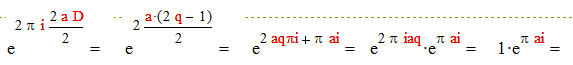Что и требовалось.

Лемма 2.

Если D и D взаимно простые числа, то

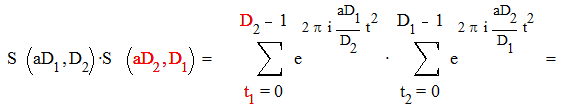S ( aD₁ , D₂ ) S ( aD₂ , D₁ ) = S ( a , D₁ D₂ )

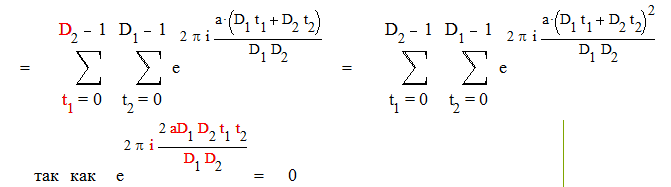Доказательство:

В этих суммах t₁ пробегает полную систему вычетов по модулю D₂ , а t₂ пробегает полную систему вычетов по модулю D_2. При этом D₁ t₁ + D₂ t₂ пробегает полную систему вычетов по модулю D₁ D₂ . Действительно , всего членов в сумме D₁ D₂ и никакие два несравнимы между собой. Действительно, предположим противное : пусть D₁ t₁ + D₂ t₂ = D₁ t₁ + D₂ t₂ ( mod D₁ D₂ )

--> ЧИТАТЬ ПОЛНОСТЬЮ <--