Реферат: Элементы сферической геометрии
На протяжении многих веков человечество не переставало пополнять свои научные знания в той или иной области науки. Стереометрия, как наука о фигурах в пространстве, неотъемлемо связана со многими из научных дисциплин. К таким дисциплинам относятся: математика, физика, информатика и программирование, а также химия и биология. В последних стоит проблема изучения микромира, который представляет собой сложнейшую комбинацию различных частиц в пространстве относительно друг друга. В архитектуре постоянно используются теоремы и следствия из стереометрии.
Множество учёных геометров, да и простых людей, интересовались такой фигурой как шар и его «оболочкой», носящей название сфера. Удивительно, но шар является единственным телом, обладающим меньшей площадью поверхности при объёме, равном объёму других сравниваемых тел, таких как куб, призма или прочие всевозможные многогранники. С шарами мы имеем дело ежедневно. К примеру, почти каждый человек пользуется шариковый ручкой в конец стержня которой вмонтирован металлический шар, вращающийся под действием сил трения между ним и бумагой и в процессе поворота на своей поверхности шар «выносит» очередную порцию чернил. В автомобильной промышленности изготавливаются шаровые опоры, являющиеся очень важной деталью в автомобиле и обеспечивающей правильный поворот колёс и устойчивость машины на дороге. Элементы машин, самолётов, ракет, мотоциклов, снарядов, плавательных судов, подвергающиеся постоянным воздействиям воды или воздуха, преимущественно имеют какие либо сферические поверхности, называемые обтекателями.
Приращение знаний о шаре и сфере привело к возникновению нового раздела математики — сферической геометрии, в которой изучаются фигуры, расположенные на сфере. В своей работе постараюсь изложить основные элементы сферической геометрии, рассмотреть важнейшие закономерности в этой области знания.
Объектом работы является сферическая геометрия как один из разделов геометрии. Предмет работы — основные закономерности и особенности сферической геометрии.
Цель работы — выявить основные элементы сферической геометрии и описать важнейшие положения данной области научного знания.
Для осуществления цели необходимо решить ряд задач:
Охарактеризовать специфику сферической геометрии как области математики;
Определить основные понятия сферической геометрии;
Описать важнейшие положения сферической геометрии;
Рассмотреть особенности фигур, расположенных на сфере.
Структура работы обусловлена целью и задачами исследования. Работа состоит из введения, двух глав, разбитых на параграфы, заключения и списка литературы.
Глава 1. Шар и сфера
1.1. Шар и шаровая поверхность
Шаровой или сферической поверхностью называется геометрическое место точек пространства, удаленных от данной точки О (центра) на заданное расстояние R (радиус). Все пространство по отношению к данной шаровой поверхности разбивается на внутреннюю область (куда можно присоединить и точки самой поверхности) и внешнюю. Первая из этих областей называется шаром. Итак, шар — геометрическое место всех точек, удаленных от заданной точки О (центра) на расстояние, не превышающее данной величины R (радиуса). Шаровая поверхность является границей, отделяющей шар от окружающего пространства.
Шаровую поверхность и шар можно получить также, вращая окружность (круг) вокруг одного из диаметров.
Рассмотрим окружность с центром О и радиусом R (рис. 1), лежащую в плоскости λ. Будем вращать ее вокруг диаметра АВ. Тогда каждая из точек окружности, например М, в свою очередь опишет при вращении окружность, имеющую своим центром точку М0—проекцию вращающейся точки М на ось вращения АВ. Плоскость этой окружности перпендикулярна к оси вращения. Радиус ОМ, ведущий из центра исходной окружности в точку М, будет сохранять свою величину во все время вращения, и потому точка М все время будет находиться на сферической поверхности с центром О и радиусом R. Шаровая поверхность может быть получена вращением окружности вокруг любого из ее диаметров.
Сам шар как тело получается вращением круга; ясно, что для получения всего шара достаточно вращать полукруг около ограничивающего его диаметра.
Эти геометрические объекты, так же как окружность и круг, рассматривали еще в глубокой древности. Открытие шарообразности Земли, появление представлений о небесной сфере дали толчок к развитию специальной науки – сферики (сферическая геометрия), изучающей расположенные на сфере фигуры.
1.2. Сферическая геометрия
Сферическая геометрия - раздел математики, в котором изучаются фигуры, расположенные на сфере. Она представляет собой своеобразный мост между планиметрией и стереометрией, так как сферические многоугольники получаются в пересечении сферы с многогранными углами с вершинами в центре сферы, сферические окружности – в пересечении сферы с коническими поверхностями и т.д. Сферическая геометрия возникла в связи с потребностями астрономии. По-видимому, первым обращением человечества к тому, что потом получит название сферической геометрии, была планетарная теория греческого математика Евдокса (ок. 408–355гг. до н.э.), одного из учеников Академии Платона. Это была попытка объяснить движение планет вокруг Земли с помощью четырех вращающихся концентрических сфер, каждая из которых имела особую ось вращения с концами, закрепленными на охватывающей сфере, к которой, в свою очередь, были «прибиты» звезды. Таким образом объяснялись замысловатые траектории планет (в переводе с греческого «планета» – блуждающая). Именно благодаря такой модели древнегреческие ученые умели достаточно точно описывать и предсказывать движения планет. Это было необходимо, например, в мореплавании, а так же во многих других «земных» задачах, где нужно было учитывать, что Земля – не плоский блин, покоящийся на трех китах.
Значительный вклад в сферическую геометрию внес Менелай из Александрии жившего в 1 веке. Его труд Сферика стал вершиной достижений греков в этой области. В Сферике рассматриваются сферические треугольники – предмет, которого нет у Евклида. Менелай перенес на сферу евклидову теорию плоских треугольников и в числе прочего получил условие, при котором три точки на сторонах сферического треугольника или их продолжениях лежат на одной прямой. Соответствующая теорема для плоскости в то время была уже широко известна, однако в историю геометрии она вошла именно как теорема Менелая, причем, в отличие от Птолемея, у которого в работах немало вычислений, трактат Менелая геометричен строго в духе евклидовой традиции.
Таким образом, потребности человека в астрономических знаниях, привели к возникновению особой области математической науки — сферическая геометрия. Эта наука получила широкое распространение в настоящее время.
Глава 2. Элементы сферической геометрии
2.1. Основные положения сферической геометрии
Именно большим окружностям и отводится роль прямых в сферической геометрии. Как правило, через две точки на сфере, как и на плоскости, можно провести только одну сферическую прямую. Исключение составляют диаметрально противоположные точки: например, через полюсы на глобусе проходит бесконечно много меридианов. Всякая плоскость, пересекающая сферу, дает в сечении окружность. Если плоскость проходит через центр сферы, то в сечении получается так называемый большой круг. Через любые две точки на сфере, кроме диаметрально противоположных, можно провести единственный большой круг. (На глобусе примером большого круга служит экватор и все меридианы.) Через диаметрально противоположные точки проходит бесконечное количество больших кругов. Меньшая дуга AmB (рис. 2) большого круга является кратчайшей из всех линий на сфере, соединяющих заданные точки. Такая линия называется геодезической.
Рис.2
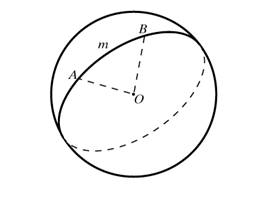
Геодезические линии играют на сфере ту же роль, что и прямые в планиметрии. Многие положения геометрии на плоскости справедливы и на сфере, но, в отличие от плоскости, две сферические прямые пересекаются в двух диаметрально противоположных точках. Таким образом, в сферической геометрии просто не существует понятия параллельности. Еще одно отличие – сферическая прямая замкнута, т.е. двигаясь по ней в одном и том же направлении, мы вернемся в исходную точку, точка не разбивает прямую на две части. Вот ещё удивление сферической геометрии: треугольник на сфере может иметь сразу три прямых угла, если, например, он ограничен двумя перпендикулярными меридианами и экватором.
Рис.3
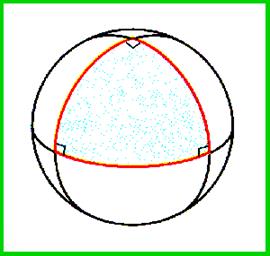
Теперь познакомимся с понятиями сферической геометрии. При этом мы будем постоянно сравнивать их с понятиями обычной геометрии.
--> ЧИТАТЬ ПОЛНОСТЬЮ <--