Реферат: Элементы сферической геометрии

2.5. Сферическая тригонометрия

Сферическая тригонометрия – раздел тригонометрии, в котором изучаются зависимости между величинами углов и длинами сторон треугольников, а также алгебраическими тождествами тригонометрических функций применительно к сферическим треугольникам. Применяется для решения различных геодезических и астрономических задач.

Пусть А, В, С - углы и а, b, с - противолежащие им стороны сферического треугольника ABC (рис.12 ). Углы и стороны сферического треугольника связаны следующими основными формулами Сферическая тригонометрия :

cos а = cos b cos с + sin b sin с cos А,

cos A = - cos B cos С + sin B sin С cos a,

sin a cos B = cos b sin c - sin b cos с cos А,

sin А cos b = cos B sin C + sin B cos С cos a;

рис.12

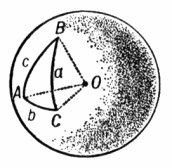
В этих формулах стороны а, b, с измеряются соответствующими центральными углами.

Для прямоугольных сферических треугольников (А = 90`, а - гипотенуза, b, с- катеты) формулы Сферической тригонометрии упрощаются, например:

sin b = sin a sin В,

cos a = cos b cos c,

sin a cos B = cos b sin c.

Формулы Сферической тригонометрии позволяют по любым трём элементам сферического треугольника определить три остальные (решить треугольник).

Рассмотренные элементы сферической геометрии дают нам обобщенное представление о данной области математической науки.

2.6. Применение сферической геометрии на практике

Сферическая геометрия нужна не только астрономам, штурманам морских кораблей, самолетов, космических кораблей, которые по звездам определяют свои координаты, но и строителям шахт, метрополитенов, тоннелей, а также геодезических съемках больших поверхностях земли, когда становится необходимым учитывать ее шарообразность.

Заключение

Подводя итоги проделанной работе, необходимо отметить, что в данной работе удалось: охарактеризовать специфику сферической геометрии как области математики на основе исторических фактов, определить основные понятия сферической геометрии, рассмотреть особенности фигур, расположенных на сфере, ознакомиться с главными учеными исследуемых сферическую геометрию в своих работах. Изучая особенности сферической геометрии, производилось сравнение с планиметрией и стереометрией.

Так же в работе было ознакомление, из каких потребностей возникла наука – сферическая геометрия, ее практическое применения в различных сферах знаний. Все это доказывает актуальность этого раздела математике в жизни человека.

Надеюсь, что и мне пригодятся эти знания при дальнейшем изучении геометрии в высшем учебном заведении.

Список литературы

Адамар Ж. Элементарная геометрия. – Ч.2.: Стереометрия : Пособие – 3-е изд. – М.: Учпедгиз, 1998.- 760 с.

АбрамовА.М, Виленкин Н.Я, ДорофеевГ.В, и др Избранные вопросы математики10 кл.: Факультативный курс./Под ред. ФирсоваВ.В/-М. : Просвещение 1992.

Александров.А.Д. и др.Геометрия для 10-11 классов Учебное пособие для учащихся школ и классов с углубленным изучением математики./А.Д. Александров, А.Л.Вернер, В.И.Рыжик. - 3-е изд., перераб.-М.: Просвещение, 1992.- 464с.

Атанасян Л.С. Геометрия: учебник для 10-11 классов средней школы.-М: Просвещение, 2007.- 208 с.

Гильберт Д. Кон-Фоссен С. Наглядная геометрия: Пер. с нем. – 3-е изд. – М.: Наука, 1981.- 344 с.

Глаголев Н. А. Проективная геометрия: Учеб. Пособие. – 2 –ое изд. испр. и доп. – М.: высш. школа, 1990. – 344 с.

Давидов А. Начала тригонометрии: 3-е изд., 1885.