Реферат: Энтропия
К. Шенноном доказана теорема о единственности меры количества информации. Для случая равномерного закона распределения плотности вероятности мера Шеннона совпадает с мерой Хартли. Справедливость и достаточная универсальность формул Хартли и Шеннона подтверждается и данными нейропсихологии.
Пример. Время t реакции испытуемого на выбор предмета из имеющихся N предметов линейно зависит от log2 N: t=200+180log2 N (мс). По аналогичному закону изменяется и время передачи информации в живом организме. В частности, один из опытов по определению психофизиологических реакций человека состоял в том, что перед испытуемым большое количество раз зажигалась одна из n лампочек, которую он должен указать. Оказалось, что среднее время, необходимое для правильного ответа испытуемого, пропорционально не числу n лампочек, а именно величине I определяемой по формуле Шеннона, где pi - вероятность зажечь лампочку номер i.
Сообщение о наступлении события с меньшей вероятностью несёт в себе больше информации, чем сообщение о наступлении события с большей вероятностью. Сообщение о наступлении достоверно наступающего события несёт в себе нулевую информацию (и это вполне ясно, - событие всё равно произойдёт когда-либо).
Если в формуле Шеннона обозначить fi = —n log2 pi , то получим, что I можно понимать как среднеарифметическое величин fi .
Отсюда, fi можно интерпретировать как информационное содержание символа алфавита с индексом i и величиной pi вероятности появления этого символа в сообщении, передающем информацию.
Основными положительными сторонами формулы Шеннона является её отвлечённость от семантических и качественных, индивидуальных свойств системы, а также то, что в отличие от формулы Хартли она учитывает различность, разновероятность состояний - формула имеет статистический характер (учитывает структуру сообщений), делающий эту формулу удобной для практических вычислений. Основные отрицательные стороны формулы Шеннона: она не различает состояния (с одинаковой вероятностью достижения, например), не может оценивать состояния сложных и открытых систем и применима лишь для замкнутых систем, отвлекаясь от смысла информации.
Увеличение (уменьшение) меры Шеннона свидетельствует об уменьшении (увеличении) энтропии (организованности) системы. При этом энтропия может являться мерой дезорганизации систем от полного хаоса (S=Smax) и полной информационной неопределённости (I=Imin) до полного порядка (S=Smin) и полной информационной определённости (I=Imax) в системе.
Пример. Чем ближе движущийся объект к нам, тем полнее информация обрабатываемая нашими органами чувств, тем чётче и более структурирован (упорядочен) объект. Чем больше информации мы имеем о компьютерной технике, тем меньше психологический барьер перед ним (согласно основному соотношению между энтропией и информацией).
3. Термодинамическая мера. Информационно-термодинамический подход связывает величину энтропии системы с недостатком информации о её внутренней структуре (не восполняемым принципиально, а не нерегистрируемым). При этом число состояний определяет, по существу, степень неполноты наших сведений о системе.
Пусть дана термодинамическая система (процесс) S, а Н0 , Н1 - термодинамические энтропии системы S в начальном (равновесном) и конечном состояниях термодинамического процесса, соответственно. Тогда термодинамическая мера информации (негэнтропия) определяется формулой:
Н(Н0 ,Н1 )=Н0 — Н1 .
Эта формула универсальна для любых термодинамических систем. Уменьшение Н(Н0 ,Н1 ) свидетельствует о приближении термодинамической системы S к состоянии статического равновесия (при данных доступных ей ресурсах), а увеличение - об удалении.
Поставим некоторый вопрос о состоянии некоторой термодинамической системы. Пусть до начала процесса можно дать p1 равновероятных ответов на этот вопрос (ни один из которых не является предпочтительным другому), а после окончания процесса - p2 ответов. Изменение информации при этом:
D I = k ln(p1 / p2 ) = k (ln p1 — ln p2 ).
Если p1 > p2 (D I >0) - прирост информации, т.е. сведения о системе стали более определёнными, а при p10 - более низкой организации).
Термодинамическая мера (энтропия) применима к системам, находящимся в тепловом равновесии. Для систем, далёких от теплового равновесия, например, живых биосистем, мера - энтропия - менее подходящая.
4. Энергоинформационная (квантово-механическая) мера. Энергия (ресурс) и информация (структура) - две фундаментальные характеристики систем реального мира, связывающие их вещественные, пространственные, временные характеристики. Сейчас актуально говорить о биоэнергоинформационных мерах, отражающих механизм взаимосвязей биофизикоинформационных и вещественно-энергетических процессов в системе, в ноосфере.
3. Теорема Шеннона о кодировании при наличии помех
Рассмотрим первую теорему Шеннона. Первая теорема Шеннона о передаче информации, которая называется также основной теоремой о кодировании при отсутствии помех, формулируется следующим образом: п ри отсутствии помех передачи всегда возможен такой вариант кодирования сообщения, при котором среднее число знаков кода, приходящихся на один знак кодируемого алфавита, будет сколь угодно близко к отношению средних информаций на знак первичного и вторичного алфавитов.
Используя понятие избыточности кода, можно дать более короткую формулировку теоремы: при отсутствии помех передачи всегда возможен такой вариант кодирования сообщения, при котором избыточность кода будет сколь угодно близкой к нулю.
Данные утверждения являются теоремами и, следовательно, должны доказываться, однако доказательства мы опустим. Для нас важно, что теорема открывает принципиальную возможность оптимального кодирования. Однако необходимо сознавать, что из самой теоремы никоим образом не следует, как такое кодирование осуществить практически – для этого должны привлекаться какие-то дополнительные соображения, что и станет предметом нашего последующего обсуждения.
Далее в основном ограничим себя ситуацией, когда M = 2, т.е. для представления кодов в линии связи используется лишь два типа сигналов – с практической точки зрения это наиболее просто реализуемый вариант (например, существование напряжения в проводе (будем называть это импульсом) или его отсутствие (пауза); наличие или отсутствие отверстия на перфокарте или намагниченной области на дискете); подобное кодирование называется двоичным. Знаки двоичного алфавита принято обозначать "0" и "1", но нужно воспринимать их как буквы, а не цифры. Удобство двоичных кодов и в том, что при равных длительностях и вероятностях каждый элементарный сигнал (0 или 1) несет в себе 1 бит информации (log2 M = 1); тогда из (1), теоремы Шеннона:
I1(A)![]() K(2)
K(2)
и первая теорема Шеннона получает следующую интерпретацию: при отсутствии помех передачи средняя длина двоичного кода может быть сколь угодно близкой к средней информации, приходящейся на знак первичного алфавита.
Применение формулы (2) для двоичного кодирования дает:
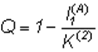
Определение количества переданной информации при двоичном кодировании сводится к простому подсчету числа импульсов (единиц) и пауз (нулей). При этом возникает проблема выделения из потока сигналов (последовательности импульсов и пауз) отдельных кодов. Приемное устройство фиксирует интенсивность и длительность сигналов. Элементарные сигналы (0 и 1) могут иметь одинаковые или разные длительности. Их количество в коде (длина кодовой цепочки), который ставится в соответствие знаку первичного алфавита, также может быть одинаковым (в этом случае код называется равномерным) или разным (неравномерный код). Наконец, коды могут строиться для каждого знака исходного алфавита (алфавитное кодирование) или для их комбинаций (кодирование блоков, слов). В результате при кодировании (алфавитном и словесном) возможны следующие варианты сочетаний:
Таблица 1.
| Варианты сочетаний длительности элементарных сигналов | Кодировка первичных символов (слов) | Ситуация |
| одинаковые | равномерная | (1) |
| одинаковые | неравномерная | (2) |
| разные | равномерная | (3) |
| разные | неравномерная | (4) |
В случае использования неравномерного кодирования или сигналов разной длительности (ситуации (2), (3) и (4)) для отделения кода одного знака от другого между ними необходимо передавать специальный сигнал – временной разделитель (признак конца знака) или применять такие коды, которые оказываются уникальными, т.е. несовпадающими с частями других кодов. При равномерном кодировании одинаковыми по длительности сигналами (ситуация (1)) передачи специального разделителя не требуется, поскольку отделение одного кода от другого производится по общей длительности, которая для всех кодов оказывается одинаковой (или одинаковому числу бит при хранении).
Длительность двоичного элементарного импульса (![]() ) показывает, сколько времени требуется для передачи 1 бит информации. Очевидно, для передачи информации, в среднем приходящейся на знак первичного алфавита, необходимо время
) показывает, сколько времени требуется для передачи 1 бит информации. Очевидно, для передачи информации, в среднем приходящейся на знак первичного алфавита, необходимо время ![]() . Таким образом, задачу оптимизации кодирования можно сформулировать в иных терминах: построить такую систему кодирования, чтобы суммарная длительность кодов при передаче (или суммарное число кодов при хранении) данного сообщения была бы наименьшей.
. Таким образом, задачу оптимизации кодирования можно сформулировать в иных терминах: построить такую систему кодирования, чтобы суммарная длительность кодов при передаче (или суммарное число кодов при хранении) данного сообщения была бы наименьшей.
§4. Пример использования энтропии в прогнозировании и ее значение для прогнозирования. Применение к рискам
Прогнозирование — частный вид моделирования как основы познания и управления.
Роль прогнозирования в управлении страной, отраслью, регионом, предприятием очевидна. Необходимы учет СТЗП-факторов (социальных, технологических, экономических, политических), факторов конкурентного окружения и научно-технического прогресса, а также прогнозирование расходов и доходов предприятий и общества в целом (в соответствии с жизненным циклом продукции — во времени и по 11-ти стадиям международного стандарта ИСО 9004). Проблемы внедрения и практического использования математических методов эконометрического прогнозирования связаны прежде всего с отсутствием в нашей стране достаточно обширного опыта подобных исследований, поскольку в течение десятилетий планированию отдавался приоритет перед прогнозированием.