Реферат: Фильтрование воды
где ΔC1 — уменьшение концентрации частиц за счет их прилипания; ΔС2 — увеличение концентрации за счет отрыва частиц.
Снижение концентрации частиц за счет их прилипания может быть принято пропорциональным средней концентрации частиц в объеме выделенного слоя С и оно пропорционально толщине слоя Ад;
![]() (12.3)
(12.3)
где b— параметр фильтрования, определяющий интенсивность прилипания частиц и зависящий от условий фильтрования.
Рост концентрации за счет отрыва ранее прилипших частиц может быть принят пропорционально количеству накопившегося к данному моменту времени осадка р Ах. Кроме того, обратно пропорционален количеству воды, проходящей через слой за единицу времени:
![]() (12.4)
(12.4)
где р — плотность насыщения загрузки осадком, т. е. массовое количество осадка, накопившееся к данному моменту времени в единице объема элементарного слоя загрузки; а — параметр фильтрования, определяющий интенсивность отрыва частиц и зависящий от условий фильтрования; v— скорость фильтрования.
Подставив значения ΔC,ΔС1 и ΔС2 в равенство (12.2), получим
![]() (12.5)
(12.5)
Уравнение (12.5) является основным уравнением, отражающим специфику процесса фильтрования суспензий через зернистую загрузку. В уравнение (12.5) входят две зависимые переменные величины Си ρ, поэтому одного этого уравнения недостаточно для описания процесса.
Вторым, дополняющим его уравнением является уравнение баланса вещества. Через поперечное сечение выделенного слоя с единичной площадью за единицу времени проходит объем воды, равный скорости фильтрования. Следовательно, массовое количество вещества задерживаемого слоем, равно
![]() ( 2.6)
( 2.6)
Извлекаемые слоем из воды частицы образуют осадок на зернах слоя, накапливающийся в ходе процесса. Количество отложений в слое толщиной Δx; составляет ρ*Δх, а скорость накопления отложений в слое или количество вещества, накапливающегося в нем за единицу времени t,равно
![]() (12.7)
(12.7)
Приравнивая выражения (12.6) и (12.7), получим
![]() '
'
Дифференциальное уравнение (12.8) является уравнением баланса веществ. Оно показывает, что количество вещества, извлеченного слоем Ах из воды за единицу времени, равно количеству накопившегося в этом слое вещества за тот же промежуток времени.
Дифференцируя уравнение (12.5) по времени и учитывая уравнение баланса (12.8), получим
![]() (12.9)
(12.9)
Это уравнение в дифференциальной форме описывает кинетику процесса осветления при фильтровании суспензий. Аналогично уравнению (12.9) получим дифференциальное уравнение для плотности насыщения
![]() (12.10)
(12.10)
описывающее в дифференциальной форме процесс изменения плотности насыщения фильтрующей загрузки осадком по ее высоте с течением времени. Выражения (12.9) и (12.10) интегрируются, но решение получается в виде бесконечного ряда и его трудно использовать для практических расчетов, которые упрощаются, если воспользоваться критериями подобия для процесса осветления, получаемыми из анализа дифференциального уравнения (12.9). С этой целью преобразуем уравнение (12.9), введя безразмерное отношение мгновенной концентрации к начальной концентрации частиц в воде, поступающей на фильтр: У=С/С0 . Тогда
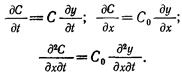
Подставляя эти значения в уравнение (12.9) и сокращая по- сТО янный множитель С0 , получим
![]() (12.11)
(12.11)
Введем теперь новые независимые безразмерные переменные
X = bx, Т = at(12.12)
![]()
Подставляя эти значения в уравнение (12.11) и сокращая постоянные множители а и b, получим