Реферат: Фильтры нижних частот
Рисунок 2.
Именно эти зависимости являются исходными при аппроксимации.
1. Полиномиальные ФНЧ с максимально плоскими характеристиками затухания (Баттерворта)
Полиномиальными называются ФНЧ, у которых ОПФ имеет вид:
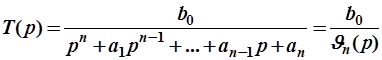 (1)
(1)
Не трудно показать, что нормированная АЧХ полиномиального фильтра определяется следующим выражением:
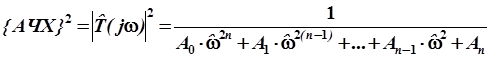 (2)
(2)
Осуществим аппроксимацию по Тейлору АЧХ фильтра нижних частот.
При этом потребуем, чтобы в точке ![]() =0, функция
=0, функция ![]() была равна единице, а все её │n-1│ первых производных обращались бы в нуль. В этом случае АЧХ синтезируемого фильтра будет максимально плоской.
была равна единице, а все её │n-1│ первых производных обращались бы в нуль. В этом случае АЧХ синтезируемого фильтра будет максимально плоской.
Решение аппроксимации даёт следующий результат:
An =1; A1 =A2 =...=An -1 =0; A0 >0,
то есть любое вещественное положительное число (в противном случае нарушается УФР).
Следовательно, а(![]() ) = 10lg
) = 10lg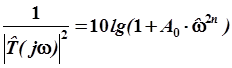 (дБ).
(дБ).
Чрезвычайно удобно положить А0 =(100,1Δа –1), где Δа - допустимая неравномерность затухания в полосе пропускания.
Так, при Δа = 3дБ получается100,1*3 =100,3 =2, следовательно А0 =1 и формула приобретает вид:
a(![]() ) = 10lg(1+
) = 10lg(1+![]() 2 n )
2 n )
нормирующая частота ω0 в таком случае выбирается из условия:
а = Δа=3дБ.
Эту частоту принято называть граничной частотой ПП фильтра. На рисунке 3 приведено семейство АЧХ ![]() для разных значений n.
для разных значений n.
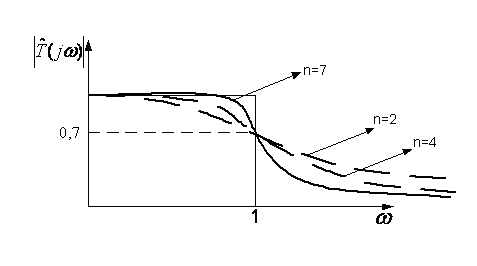
Рисунок 3.
Из него следует, что чем выше n, тем точнее аппроксимируется характеристика идеального фильтра.
Затухание рассматриваемых фильтров:
а = 10lg(1+![]() 2 n )
2 n )
в полосе задерживания, где ![]() >>1 приближенно равно а
>>1 приближенно равно а![]() 20nlg
20nlg![]() и возрастает со скоростью 6n дБ/октаву.(Октава – удвоение частоты).
и возрастает со скоростью 6n дБ/октаву.(Октава – удвоение частоты).
Если заданы требования к ФНЧ, то выбор порядка фильтра при Δа = 3дБ осуществляется из условия, которое следует из графика на рисунке 4.

Рисунок 4.
В случае, когда Δа![]() 3дБ и а0
3дБ и а0![]() 10дБ, порядок фильтра может быть подсчитан по формуле:
10дБ, порядок фильтра может быть подсчитан по формуле: