Реферат: Функции алгебры логики. Логический базис
Радиоэлектроника в настоящее время во многом определяет научно- технический прогресс и объединяет ряд отдельных областей науки и техники, развившихся из радиотехники и электроники.
Радиотехника - область науки и техники, связанная с разработкой устройств и систем, обеспечивающих генерирование, усиление, преобразование, хранение, а также излучение и прием электромагнитных колебаний радиочастотного диапазона, используемых для передачи информации.
В современных радиотехнических системах и комплексах до 90% разрабатываемых устройств реализуется на элементах цифровой и вычислительной техники и используются цифровые методы обработки сигналов.
В настоящее время бурно развивается по экспоненциальному закону вычислительная техника и ее элементная база. А не так давно первые интегральные микросхемы (1958 год) содержали до десяти транзисторов. Сегодня современные микропроцессоры содержат до 10 миллионов транзисторов на один кристалл, и менее чем через десять лет это число достигнет 100 миллионов транзисторов.
Уже отошла в историю дискретная схемотехника, когда различные узлы строились на печатных платах с использованием отдельных навесных радиоэлектронных компонентов: транзисторов, резисторов, конденсаторов и других элементов. Ранее соединения выполнялись с помощью внешнего печатного монтажа, теперь соединения и монтаж осуществляется внутри кристалла. Поэтому современный инженер электронной техники должен владеть передовыми методами и технологиями, чтобы уметь приспособить их завтра к вычислительной технике будущих поколений, овладеть практическими приемами проектирования устройств на программируемых логических интегральных схемах.
Логические выражения n двоичных переменных с помощью конечного числа логических операций можно рассматривать как некоторую функцию, отражающую взаимную связь между входными и выходными переменными. Логические операции конъюнкции ![]() и дизъюнкции
и дизъюнкции ![]() можно представить простейшими функциями вида:
можно представить простейшими функциями вида: ![]() и
и ![]() . Эти функции называются аналогично логическим операциям – функциями И и ИЛИ.
. Эти функции называются аналогично логическим операциям – функциями И и ИЛИ.
Такие ФАЛ подобно логическим выражениям могут быть заданы аналитическим и табличным способами.
При аналитическом способе ФАЛ задается в виде логических выражений, получаемых путем логических преобразований с помощью законов и правил Булевой алгебры.
При табличном способе ФАЛ задается таблицей истинности, где число всех возможных наборов (комбинаций) аргументов конечно. Если число аргументов ФАЛ равно n, то число их возможных наборов ![]() , а число различных функций
, а число различных функций ![]() , тогда при n=2, F=16. Составим таблицу истинности для функций двух аргументов.
, тогда при n=2, F=16. Составим таблицу истинности для функций двух аргументов.
Таблица 1.
| Аргументы | Функции | ||||||||||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
В таблице 1 приведены элементарные ФАЛ ![]() двух аргументов. В левой части таблицы перечислены все возможные наборы аргументов
двух аргументов. В левой части таблицы перечислены все возможные наборы аргументов ![]() и
и ![]() , в правой части приведены значения ФАЛ на соответствующих входных наборах. Значения всей совокупности этих наборов переменных представлены в таблице последовательностью чисел в двоичной системе счисления.
, в правой части приведены значения ФАЛ на соответствующих входных наборах. Значения всей совокупности этих наборов переменных представлены в таблице последовательностью чисел в двоичной системе счисления.
Каждая ФАЛ ![]() обозначает одну из 16 возможных логических операций над двумя переменными
обозначает одну из 16 возможных логических операций над двумя переменными ![]() и
и ![]() , имеет свою таблицу истинности, собственное название и условное обозначение.
, имеет свою таблицу истинности, собственное название и условное обозначение.
Основные сведения об элементарных функциях ![]() даны в таблице 2. Таблицы истинности для каждой ФАЛ составляются отдельно по таблице 1.
даны в таблице 2. Таблицы истинности для каждой ФАЛ составляются отдельно по таблице 1.
Таблица 2
| Операционные символы | Обозначения, названия | Зарубежные аналоги | |
| 0 | Константа 0 | Const 0 | |
PeersF. | |||
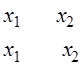 | |||
| Implicator | |||
| 1 |
Генератор 1 |
Generator 1 |
В таблице 2 часто применяемыми являются функции:
![]() -повторители 1-го и 2-го аргументов;
-повторители 1-го и 2-го аргументов;
![]() – инверсии 1-го и 2-го аргументов;
– инверсии 1-го и 2-го аргументов;
![]() – функция И (конъюнкция), логическое умножение;
– функция И (конъюнкция), логическое умножение;
![]() – функция И-НЕ (базис Шеффера);
– функция И-НЕ (базис Шеффера);
![]() – функция ИЛИ (дизъюнкция), логическое сложение;
– функция ИЛИ (дизъюнкция), логическое сложение;
![]() – функция ИЛИ-НЕ (базис Пирса);
– функция ИЛИ-НЕ (базис Пирса);
![]() – функция неравнозначности, реализуется ЛЭ “Исключающее ИЛИ” (сумматор по модулю два);
– функция неравнозначности, реализуется ЛЭ “Исключающее ИЛИ” (сумматор по модулю два);
![]() – функция равнозначности реализуется ЛЭ “Исключающее ИЛИ-НЕ”.
– функция равнозначности реализуется ЛЭ “Исключающее ИЛИ-НЕ”.
Рассмотренные элементарные функции двух аргументов ![]() играют важную роль при преобразованиях сложных логических выражений, а также при преобразовании функциональных цифровых узлов.
играют важную роль при преобразованиях сложных логических выражений, а также при преобразовании функциональных цифровых узлов.
Функции n переменных, значения которых заданы во всех точках области определения, считаются полностью определенными ФАЛ. Если какая-либо функция имеет запрещенные наборы переменных и ее значения на указанных наборах не определены, то такая ФАЛ называется не полностью определенной. Такие наборы будем отмечать в таблицах истинности (*) и при необходимости доопределять их значениями 0 и 1. Эти вопросы будут рассматриваться позже.
Логические функции, которые считаются полностью определенными, могут быть представлены различными формами.
ДНФ – дизъюнктивная нормальная форма записи ФАЛ представляется в виде суммы (дизъюнкции) ряда элементарных членов (минтермов), каждый из которых является произведением (конъюнкцией) аргументов или их инверсий. Термин “нормальная форма” предполагает, что в логическом выражении, задающем функцию, последовательно выполняются не более двух базовых операций (кроме инверсии).
Запишем ФАЛ в ДНФ:
![]() ; (1)
; (1)
Функцию (3.19) можно записать в виде дизъюнкции минтермов:
![]() ,
,
где ![]() - конъюнкции аргументов ФАЛ, называемые минтермами.
- конъюнкции аргументов ФАЛ, называемые минтермами.
СДНФ – совершенная дизъюнктивная нормальная форма записи ФАЛ представляется в ДНФ, где в каждом элементарном члене (минтерме), имеющем одинаковую размерность, представлены все аргументы функции или их инверсии.
--> ЧИТАТЬ ПОЛНОСТЬЮ <--