Реферат: Функція, її границя та неперервність

Точки, в яких функція неперервна, називаються точками неперервності, а точки, в яких неперервність порушується – точками розриву цієї функції.

Приклад

Неперервність функції

в довільній точці, крім точки, випливає із неперервності многочлена, синуса, квадратного кореня і умови; неперервність в точці (0;0) випливає із рівності

(п. 2).

Умові (1) неперервності можна надати іншого вигляду. Позначимо

, ,.

Величини, називають приростами аргументів x і , а– повним приростом функції в точці. З рівності (1) отримуємо:

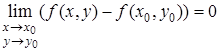
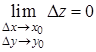.(2)

Рівність (2) дає ще одне означення неперервності.

Функція називається неперервною в точці , якщо повний приріст її в цій точці прямує до нуля, коли прирости її аргументів x та прямують до нуля.

Функція називається неперервною на множині , якщо вона неперервна в кожній точці цієї множини.

Приклад

Функція неперервна на всій площині, оскільки повний приріст цієї функції в довільній точці має вигляд

.

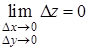Використовуючи поняття неперервності функції кількох змінних і відповідні теореми про границі, можна довести, що арифметичні операції над неперервними функціями і побудова складеної функції з неперервних функцій приводять до неперервних функцій.

Наведемо основні властивості функції, неперервної в замкненій і обмеженій області. Ці властивості аналогічні властивостям неперервної на відрізку функції однієї змінної. Попередньо уточнимо ряд понять для множин точок площини.

Множина точок площини називається зв’язною, якщо будь-які її дві точки можна з’єднати неперервною лінією, яка повністю належить множині.

Точка називається внутрішньою точкою множини, якщо існує
-окіл цієї точки, який повністю міститься у множині.

Множину називають відкритою, якщо кожна її точка внутрішня.

Областю (або відкритою областю) називають зв’язну відкриту множину точок.

Точку називають межовою точкою множини , якщо будь-який її окіл містить як точки, що належать , так і точки, що не належать множині . Множину всіх межових точок області називають межею області.

Область разом з її межею називається замкненою. Якщо існує круг скінченного радіуса, який повністю містить область, то вона називається обмеженою.

Замкнена область, в якій визначена функція двох змінних, є аналогом відрізка для функції однієї змінної.

Тепер сформулюємо властивості неперервних функцій двох змінних у замкненій обмеженій області.

1. Якщо функція неперервна в замкненій обмеженій області, то вона обмежена в цій області, тобто існує таке число , що для всіх точок області виконується нерівність.