Реферат: Функционально полные системы логических функций Алгебраический подход
Это правило является следствием распределительного закона 2-го рода и также находит широкое применение для упрощения логических функций.
Правило развертывания. Это правило регламентирует действие, обратное склеиванию. Иногда требуется представить некоторое логическое выражение в виде совокупности конституент единицы или конституент нуля. Если членами преобразуемого выражения являются элементарные конъюнкции, то переход от них к конституентам единицы производится в три этапа по следующему правилу:
· в развертываемую элементарную конъюнкцию ранга r в качестве дополнительных сомножителей вводится п- r единиц, где п — ранг конституенты;
· каждая единица представляется в виде логической суммы некоторой, не имеющейся в исходной конъюнкции переменной и ее отрицания: ![]() ;
;
· производится раскрытие всех скобок на основе распределительного закона первого рода, что приводит к развертыванию исходной элементарной конъюнкции ранга r в логическую сумму кон-ституент единицы.
Пример Развернуть элементарную конъюнкцию f(x1 ,x2 ,x3 ,x4 ) = = x 1 × x 3 в логическую сумму конституент единицы.
Решение. Ранг конституенты единицы для данной функции равен 4. Производим развертывание исходной конъюнкции поэтапно в соответствии с правилом развертывания:
1-й этап— f ( x 1 , x 2 , x 3 , x 4 ) = x 1 × 1 × x 3 × 1.
2-й этап — f ( x 1 , x 2 , x 3 , x 4 ) =![]()
3-й этап — f ( x 1 , x 2 , x 3 , x 4 )=
= ![]() что и требовалось получить.
что и требовалось получить.
Если членами преобразуемого выражения являются элементарные дизъюнкции, то переход от них к конституентам нуля производится также в три этапа по следующему правилу:
· в развертываемую элементарную дизъюнкцию ранга r в качестве дополнительных слагаемых вводится п-r нулей;
· каждый нуль представляется в виде логического произведения некоторой, не имеющейся в исходной дизъюнкции переменной, и ее отрицания:![]()
· получившееся выражение преобразуется на основе распределительного закона второго рода таким образом, чтобы произвести развертывание исходной элементарной дизъюнкции ранга r в логическое произведение конституент нуля.
Пример. Развернуть элементарную дизъюнкцию f ( x 1 , x 2 , x 3 , x 4 )= =x3 Ú x4 в логическое произведение конституент нуля.
Решение. Ранг конституенты нуля п = 4. Далее производим развертывание исходной дизъюнкции поэтапно в соответствии с правилом развертывания:
1-й этап — f ( x 1 , x 2 , x 3 , x 4 ) =0 Ú 0 Ú x3 Ú x4 ;
2-й этап — f ( x 1 , x 2 , x 3 , x 4 ) =![]()
3-йэтап— f ( x 1 , x 2 , x 3 , x 4 )=
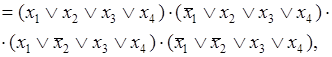
что и требовалось получить.
Проверить правильность проведенных преобразований можно при помощи правила склеивания.
3. Функционально полные системы логических функций. Анализ принадлежности переключательных функций замкнутым классам показывает, что существуют две переключательные функции f 8 и f 14 , не принадлежащие ни одному классу. Согласно теореме о функциональной полноте, каждая из этих функций образует функционально полную систему логических связей и используя только одну из них можно представить любую, сколь угодно сложную переключательную функцию.
Операция Пирса (стрелка Пирса) реализует функцию, которая принимает значение, равное единице только в том случае, когда все ее аргументы равны 0 (ИЛИ-НЕ), что может быть записано в ОФПС для функции двух переменных следующим образом:
![]() (7)
(7)
Используя операции суперпозиции и подстановки можно показать, что операция Пирса может быть реализована для n аргументов:
![]() (8)
(8)
Для представления переключательной функции в базисе Пирса необходимо выполнить следующие действия: