Реферат: Генетические алгоритмы и их практическое применение

в случае, когда она переопределена (n > m ), то иногда оказывается естественной задача о нахождении вектора x , который "удовлетворяет этой системе наилучшим образом", т. е. из всех "не решений" является лучшим.

· Задача о рационе.

o Пусть имеется n различных пищевых продуктов, содержащих m различных питательных веществ. Обозначим через a_ij содержание (долю) j -го питательного вещества в i -ом продукте, через b_j — суточную потребность организма в j -ом питательном веществе, через c_i — стоимость единицы i -го продукта. Требуется составить суточный рацион питания минимальной стоимости, удовлетворяющий потребность во всех питательных веществах

· Транспортная задача.

o Эта задача — классическая задача линейного программирования. К ней сводятся многие оптимизационные задачи. Формулируется она так. На m складах находится груз, который нужно развезти n потребителям. Пусть a_i (i = 1, ..., n ) — количество груза на i -ом складе, а b_j (j = 1, ..., m ) — потребность в грузе j -го потребителя, c_ij — стоимость перевозки единицы груза с i -го склада j -му потребителю. Требуется минимизировать стоимость перевозок.

· Задачи о распределении ресурсов.

o Общий смысл таких задач — распределить ограниченный ресурс между потребителями оптимальным образом. Рассмотрим простейший пример — задачу о режиме работы энергосистемы. Пусть m электростанций питают одну нагрузку мощности p . Обозначим через x_j активную мощность, генерируемую j -ой электростанцией. Техническими условиями определяются возможный минимум m_j и максимум M_j вырабатываемой j -ой электростанцией мощности. Допустим затраты на генерацию мощности x на j -ой электростанции равны e_j (x ). Требуется сгенерировать требуемую мощность p при минимальных затратах.[8]

Переформулируем задачу оптимизации как задачу нахождения максимума некоторой функции f(x₁ , x₂ , …, x_n ), называемой функцией приспособленности (fitness function). Она должна принимать неотрицательные значения на ограниченной области определения (для того, чтобы мы могли для каждой особи считать её приспособленность, которая не может быть отрицательной), при этом совершенно не требуются непрерывность и дифференцируемость.

Каждый параметр функции приспособленности кодируется строкой битов.

Особью будет называться строка, являющаяся конкатенацией строк упорядоченного набора параметров (рис1):

1010 10110 101 … 10101

| x1 | x2 | x3 | … | xn |

Рис 1. Ионкатенационная строка упорядоченного набора параметров

Универсальность ГА заключается в том, что от конкретной задачи зависят только такие параметры, как функция приспособленности и кодирование решений. Остальные шаги для всех задач производятся одинаково.[9]

Генетические алгоритмы оперируют совокупностью особей (популяцией), которые представляют собой строки, кодирующие одно из решений задачи. Этим ГА отличается от большинства других алгоритмов оптимизации, которые оперируют лишь с одним решением, улучшая его.[10]

С помощью функции приспособленности среди всех особей популяции выделяют:

· наиболее приспособленные (более подходящие решения), которые получают возможность скрещиваться и давать потомство

· наихудшие (плохие решения), которые удаляются из популяции и не дают потомства

Таким образом, приспособленность нового поколения в среднем выше предыдущего.[11]

В классическом ГА:

· начальная популяция формируется случайным образом

· размер популяции (количество особей N) фиксируется и не изменяется в течение работы всего алгоритма

· каждая особь генерируется как случайная L-битная строка, где L — длина кодировки особи

· длина кодировки для всех особей одинакова[12]

1.3 Алгоритм работы

На рисунке 2 изображена схема работы любого генетического алгоритма:

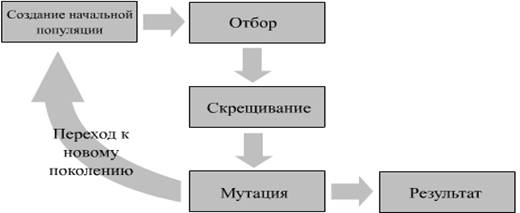
Рис 2. Схема работы любого генетического алгоритма.

Шаг алгоритма состоит из трех стадий:

1. генерация промежуточной популяции (intermediate generation ) путем отбора (selection ) текущего поколения

2. скрещивание (recombination ) особей промежуточной популяции путем кроссовера (crossover ), что приводит к формированию нового поколения

3. мутация нового поколения [13]

1.4 Отбор

Промежуточная популяция — это набор особей, получивших право размножаться. Наиболее приспособленные особи могут быть записаны туда несколько раз, наименее приспособленные с большой вероятностью туда вообще не попадут.[14]

В классическом ГА вероятность каждой особи попасть в промежуточную популяцию пропорциональна ее приспособленности, т.е. работает пропорциональный отбор (proportional selection ).

Существует несколько способов реализации данного отбора: