p₁ : 3 x₁ + x₂ = 9,

p₂ : x₁ + 2 x₂ = 8,

p₃ : x₁ + 6 x₂ = 12.

Подставляя координаты точки (0,0) в неравенства (1.8)-(1.10) видим, что начало координат им не удовлетворяет и, следовательно, не входит в множество планов Х . Поэтому штриховки направлены выше и правее граничных прямых. Выделяя точки, удовлетворяющие всем неравенствам и условиям неотрицательности, получаем множество планов, изображенное на рис. 1.2. В данном примере оно не ограничено.

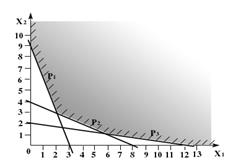
Рис. 1.2

Изобразим целевую функцию (1.7) с помощью линий уровня. Для этого достаточно построить целевой вектор c = (5, 4) и перпендикулярно ему провести несколько прямых на множестве Х. Поскольку целевой вектор указывает направление возрастания целевой функции, а в задаче о рационе требуется найти ее минимум, то для нахождения оптимального решения будем перемещать линию уровня параллельно самой себе по множеству Х в направлении, противоположном целевому вектору.

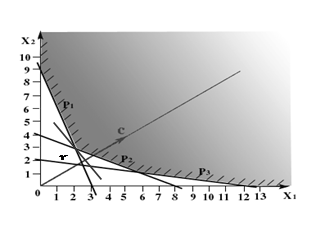
Рис. 1.3

Последней точкой множества планов, через которую еще проходит линия уровня будет точка пересечения прямых p₁ и p₂ . Решая систему уранений (рис. 1.3).

3 x₁ + x₂ = 9

x₁ + 2 x₂ = 8

получим оптимальный план x₁ * = 2, x₂ * = 3. Минимальное значение целевой функции при этом будет равно

f(x*) = 5∙2 + 4∙3 = 22.

Следовательно, самый дешевый набор для профилактического приема состоит из 2 гр . комплекса А и 3 гр . комплекса В , и его стоимость равна 22 руб.

Теперь несложно сформулировать геометрический способ решения стандартных задач ЛП с двумя переменными:

· изображается допустимый многоугольник – пересечение полуплоскостей, являющихся решениями соответствующих неравенств;

· изображается целевой вектор ;

· через допустимое множество проводится перпендикуляр к целевому вектору – это линия уровня целевой функции;

· путем перемещения линии уровня параллельно самой себе в направлении целевого вектора до тех пор, пока не окажется по одну сторону от перемещаемой прямой, визуально определяется точка (или точки) максимума;

· вычисляются координаты точки максимума (решением соответствующей системы уравнений, задающих прямые, точка пересечения которых и есть искомая точка) и максимальное значение целевой функции.

Замечание. Для определения точки минимума следует перемещать изолинию против направления целевого вектора.

В разобранных примерах оптимальный план находился в единственной вершине многоугольника допустимых планов. Однако при решении задач ЛП могут встретиться и другие случаи.

Бесконечное множество оптимальных планов. На рис.1.4 целевая функция принимает одно и то же максимальное значение в любой точке отрезка AB , соединяющего две вершины множества планов Х . Такая ситуация возникает, если линии уровня параллельны граничной прямой.

Отсутствие ограниченного решения . На рис.1.5 изображен случай, когда целевая функция не ограничена сверху на множестве планов и решение задачи на максимум не существует. При этом решение задачи на минимум может существовать, (как в задаче о витаминах).

Отсутствие допустимых планов. На рис.1.6 области, допустимые по каждому из ограничений, не имеют общих точек. В этом случае говорят, что ограничения несовместны, множество планов пусто и задача ЛП решения не имеет.

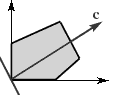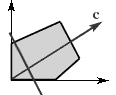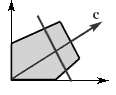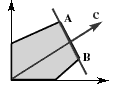
Рис. 1.4 Рис. 1.5 Рис. 1.6

2. Симплекс-метод

2.1 Идея симплекс-метода

Рассмотрим универсальный метод решения канонической задачи линейного программирования