Реферат: Графический метод и симплекс-метод решения задач линейного программирования
xБ = b .
Для базисного плана такого вида может быть сформулирован достаточно простой для проверки критерий оптимальности. Введем величины
∆j = < сБ , Aj > – cj , j = 1,...,n, (2.1)
где сБ – вектор из коэффициентов целевой функции при базисных переменных xБ , Aj – j- йстолбец матрицы условий, cj – j- й коэффициент целевой функции. Разности ∆j называются симплексными разностями или симплексными оценками.
Критерий оптимальности базисного плана . Если для базисного плана с единичной базисной матрицей все симплексные оценки неотрицательны, то этот план оптимален.
Применим данный критерий для проверки на оптимальность базисного плана x0 = (10, 0, 20, 0, 8) из примера 2.1.
Так как в этом плане вектор базисных переменных xБ =(x1 , x3 ,x5 ), то сБ = (c1 , c3 ,c5 ) = (1, 0, 2).
.
Следовательно,
∆1 = < сБ , A1 > – c1 =1∙1 + 0∙0 + 2∙0 – 1= 0,
∆2 = < сБ , A2 > – c2 =1∙3 + 0∙1 + 2∙2 – (-3) = 10,
∆3 = < сБ , A3 > – c3 =1∙0 + 0∙1 + 2∙0 – 0= 0,
∆4 = < сБ , A4 > – c4 =1∙(-1) + 0∙5 + 2∙1 – 4= -3,
∆5 = < сБ , A5 > – c5 =1∙0 + 0∙0 + 2∙1 – 2= 0.
Так как оценка ∆4 < 0, то базисный план x0 не оптимален. Заметим, что симплексные оценки, соответствующие базисным переменным, всегда равны нулю, так что достаточно проверять только небазисные оценки.
2.2 Реализация симплекс-метода на примере
Продемонстрируем применение симплекс-метода на примере. Рассмотрим каноническую задачу ЛП
| f(x) = x 1 + 2x 2 + 0 x 3 + 0 x 4 →max | (2.2) |
| –x 1 + 2x 2 + x 3 = 4, | (2.3) |
| 3 x 1 + 2x 2 + x 4 = 12, | (2.4) |
| xj ≥ 0, j = 1,2,3,4. | (2.5) |
Матрица условий A = (A 1 , A 2 , A 3 , A 4 ), где
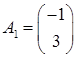
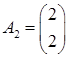
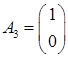
Целевой вектор c =(c1 , c2 , c3 , c4 ) = (1, 2, 0, 0); вектор правых частей b =(b 1 , b 2 ) = (4, 12).
Шаг 0. Нахождение начальной угловой точки (базисного плана).
Задача имеет предпочтительный вид, так как правые части уравнений положительны, а столбцы матрицы условий A 3, A 4 образуют единичную подматрицу. Значит начальная базисная матрица 
= (A 3 , A4 ); x 3 иx 4 – базисные переменные,x 1 иx 2 - небазисные переменные, cБ = (c 3, c 4) = = (0, 0).
Начальный базисный план имеет вид x0 = (0, 0, x 3 , x 4) = (0, 0, 4, 12); f( xo )= 0.
Шаг 1. Проверка базисного плана на оптимальность.
Подсчитаем симплексные оценки для небазисных переменных по формуле (5.1)
1 = < cБ , A 1 > – c 1 = 0 ·(–1) + 0 ·3 – 1 = –1.
2 = < cБ , A 2 > – c 2 = 0 ·2 + 0 · 2 – 2 = –2.
Так как оценки отрицательны, то план x – не оптимален. Будем искать новый базисный план (смежную угловую точку) с большим значением целевой функции.
Шаг 2 . Нахождение переменной вводимой в базис.
Целевую функцию можно увеличить, если ввести в состав базисных переменных (сделать положительной) одну из небазисных переменных x 1 илиx 2 , поскольку обе оценки j < 0. Обычно в состав базисных вводят небазисную переменную с наибольшей по модулю отрицательной оценкой, поэтому будем вводить в базис переменную x 2.