Реферат: Графовые модели. Остов минимального веса

Рисунок 9.Полученный остов на шаге 3

Шаг 4. Найдено ребро минимального веса: 3-5=11.

Рассмотрены все вершины и инцидентные ребра этим вершинам, оставшиеся образуют цикл в полученном минимальном остове. А это не удовлетворяет условиям поставленной задачи.

На четвертом шаге получили окончательный остов минимального веса, который представлен на рисунке 10.

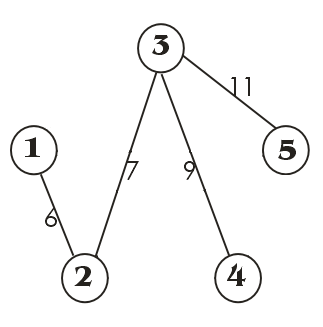
Рисунок 10. Остов минимального веса

При изменении вершины начала построения конфигурация остова минимального веса не измениться, а измениться лишь последовательность построения ребер остова.

Например, если в качестве начальной вершины выбрать четвертую вершину, то последовательность этапов построения остова минимального веса будет выглядеть следующим образом:

Шаг 1. 4-3=9;

Шаг 2. 3-2=7;

Шаг 3. 2-1=6;

Шаг 4. 3-5=11;

При этом конфигурация остова останется прежней. Решим данную задачу с помощью программной модели. Чтобы решить данную задачу необходимо построить матрицу весов, матрица представлена на рисунке 11.

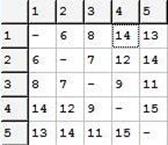
Рисунок 11. Матрица весов

Полученный минимальный остов с помощью программной модели изображен на рисунке 12.

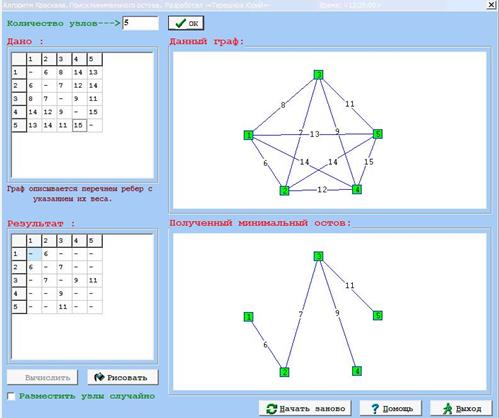
Рисунок 12. Полученный минимальный остов

После проверки вычислений вручную и программной модели результат одинаковый, это означает, что программная модель работает и функционирует верно.

Задача №2. Дан взвешенный, связный, неориентированный граф, состоящий из девяти вершин. Необходимо найти остов минимального веса с помощью алгоритма Краскала. Исходный граф на рисунке 13.

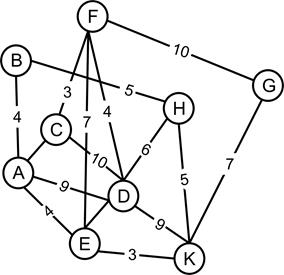
Рисунок 13. Исходный граф

Выбираем вершину начала построения остова минимального веса, например, первую вершину.

Шаг 1. Найдено ребро минимального веса: AC=1. Полученный остов на рисунок 14.

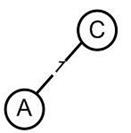
Рисунок 13. Полученный остов на шаге 1

Шаг 2. Найдено ребро минимального веса: CF=3, AB=4, AC=4. Полученный остов на рисунок 15.

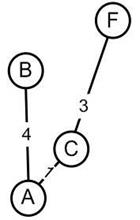
Рисунок 14. Полученный остов на шаге 2