Реферат: Графовые модели. Остов минимального веса

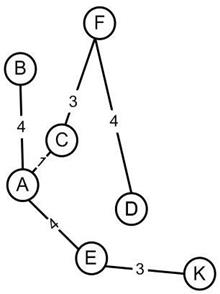
Рисунок 15. Полученный остов на шаге 3

Шаг 4. Найдено ребро минимального веса: KH=5, KG=4. Рассмотрены все вершины и инцидентные ребра этим вершинам, оставшиеся ребра образуют цикл в полученном минимальном остове. А это не удовлетворяет условиям поставленной задачи.

На четвертом шаге получен окончательный остов минимального веса, который представлен на рисунке 16.

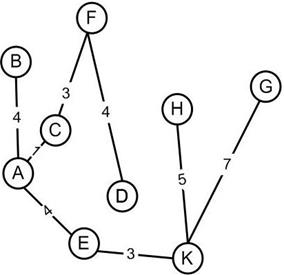
Рисунок 16. Остов минимального веса

Решим данную задачу с помощью программной модели. Чтобы решить данную задачу необходимо построить матрицу весов.

Таблица 1. Матрица весов

A	B	C	D	E	F	G	H	K
A	-	4	1	9	4	-	-	-	-
B	4	-	-	-	-	-	-	5	-
C	1	-	-	10	-	3	-	-	-
D	9	-	10	-	5	4	-	6	9
E	4	-	3	5	-	7	-	-	3
F	-	-	-	4	7	-	10	-	-
G	-	-	-	-	-	10	-	-	7
H	-	5	-	6	-	-	-	-	5
K	-	-	-	9	3	-	7	5	-

Полученный минимальный остов с помощью программной модели изображен на рисунке 17.

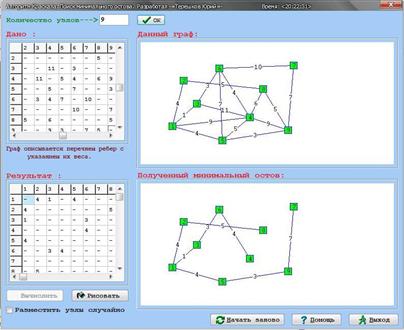
Рисунок 17. Остов минимального веса

После проверки вычислений вручную и программной модели полученные остовы минимального веса различаются, но они построены верно. Это связано с тем, что программа выбирает другую вершину начала. После решения двух контрольных задач стало ясно, что разработанная программная модель работает верно.

Заключение

Целью данного курсового проекта была задача нахождения остова минимального веса во взвешенном графе с помощью алгоритма Краскала. Есть много способов создания модели, решающей эту задачу. Могут существовать различные алгоритмы обработки графов с разными представлениями: в виде матрицы инцидентности, матрицы смежности, матрицы весов. При решении данной задачи можно изменять вершину начала поиска остова минимального веса, при этом конфигурация остова не измениться. Она может измениться при наличии ребер одинакового минимального веса.

Контрольная задача показала, что данная программная модель функционирует верно, и поэтому она может быть успешно использована в качестве наглядного пособия для изучения задачи нахождения остова минимального веса. Для эффективности изучения в программе создана подсказка для пользователя, позволяющая быстро изучить назначение компонентов. Для наглядности представления метода в программе имеется графическое изображение графа.

Список литературы

Судоплатов С.В., Овчинникова Е. В. Элементы дискретной математики: Учебник. – М.: ИНФРА-М, Новосибирск: Изд-во НГТУ,2002. – 208 с.

Кандзюба С.П., Громов В.Н. Delphi 7. Базы данных и приложения. Лекции и упражнения. – СПб: ООО «ДиаСофтЮП», 2005. – 576 с.

Богумирский Б. А. Энциклопедия Windows 98. 2-е изд. – СПб.: Питер, 2003–896 с.

Липский С.Г. «Комбинаторика для программистов»

Васильков Ю.В., Н.Н. Василькова «Компьютерные технологии вычислений в математическом моделировании», М. Финансы и Статистика, 1999

Культин Н.Б. Delphi 7 Программирование на Object Pascal. – СПб.: БХВ – Петербург, 2005. – 528 с.

Приложение А: листинг программы

unit Unit1;

interface

uses

Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,

Dialogs, Buttons, Grids, StdCtrls, ExtCtrls, ComCtrls, XPMan, Menus;

type

TForm1 = class(TForm)