Реферат: Граничні теореми теорії ймовірностей

Теорема Бернуллі. Нехай імовірність появи події А в кожному із п незалежних повторних випробувань дорівнює р, т - число появ події А (частота події) в п випробуваннях. Тоді

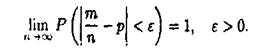
Доведення. Частість можна розглядати як невід'ємну випадкову величину. Знайдемо її математичне сподівання

Отже, необхідно оцінити імовірність відхилення випадкової величинивід її математичного сподівання. Для цього знайдемо дисперсію цієї випадкової величини

За нерівністю Чебишова одержимо

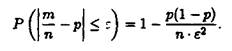
Звідси граничним переходомодержуємо (4), що й треба було довести.

Теорема Чебишова. Нехай - послідовність попарно незалежних випадкових величин, які задовольняють умовам

для усіх t= 1,2,..., п.

Тоді

Доведення. Знайдемо математичне сподівання та дисперсіюсередньої випадкових величин, тобто

Застосуємо для випадкової величини нерівність Чебишова (2)

Границя цієї імовірності при дорівнює одиниці, тобто рівність (5) доведено.

Центральна гранична теорема. Нехай задана послідовність незалежних однаково розподілених випадкових величин

Розглянемо випадкову величинуТоді

Прифункція розподілу

тобто сумабуде розподілена за нормальним законом з математичним сподіванням 0 та дисперсією

Для доведення цієї теореми треба знайти границю характеристичної функції, побудованої для нормованої випадкової величини

--> ЧИТАТЬ ПОЛНОСТЬЮ <--