Реферат: Имитационное моделирование системы "Хищник-Жертва"
При запуске программы в соответствующих полях можно ввести начальную численность хищников и жертв.
Для накопления статистических данных программа записывает численности жертв и хищников в следующие файлы D:\\Hicnic и D:\\Gertva.
Анализ модели
Для удобства анализа получаемой информации в программу добавлена функция вывода в файл, которая выводит на каждой итерации количество жертв и хищников.

Вид программы моделирующей взаимодействие
Кроме статистических выводов, данная программа позволяет получить наглядны визуальные результаты:
1. Хищники «разрезают» исходную популяцию на более мелкие популяции, которые некоторое время «развиваются» по отдельности. (Так в реальной жизни происходит накопление в популяциях различий между особями одного вида.).

Развитие двух изолированных друг от друга популяций
2. Хищники всегда следуют за жертвами (большая их часть), а жертвы очень быстро распространяются на те территории, где больше всего съестных ресурсов (травы).
Данный результат хорошо согласуется с жизнью, т.к. «отставшие» хищники обречены на голодную смерть, а переход травоядных с одного на другое место обусловлен истощением кормовых ресурсов.

Следование хищников за жертвами
Данная модель позволяет получить не только наглядное графическое представление, но и получить численности жертв и хищников в каждый момент времени.
Анализ полученных статистических данных.
1. В данной модели выполняется «насыщение» численности
При введении в систему одних жертв. Через некоторое время система приходит в равновесное состояние.
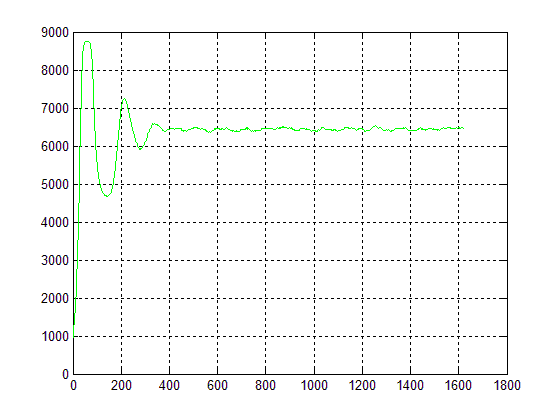
Стабилизация численности жертв к равновесной численности в условиях отсутствия хищников.
Мы получили логистическую кривую. Данный результат можно считать «хорошим знаком». Это говорит о том, что в нашей имитационной модели численность жертв ,при отсутствии хищников, хорошо согласуется с теорией (логистической моделью).
Ограничивающим фактором развития численности становится нехватка корма (травы).
Самопроизвольно выйти из этого состояния система не может.
2. Оба вида выживают.
Проведём небольшой эксперимент: когда в отсутствии хищников система стабилизируется, извне запустим в неё хищника. В результате чего получим:
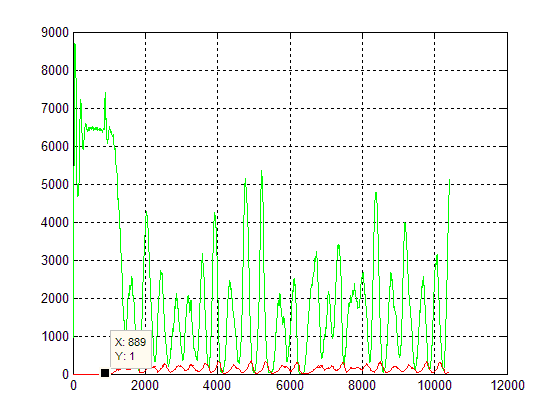
График зависимости численности жертв и хищников от времени.
Меткой показан момент времени ввода в систему одного хищника. В результате чего система выходит из положения равновесия и начинается процесс колебаний численностей. В данном случае колебания численности достаточно хорошо согласуются с моделью Лотки-Вольтерра. Вид аналитического решения
хищник жертва плоскость модель
