Реферат: Индивидуальное развитие как новая стратегия эволюции

Ряд интересных утверждений может быть высказан и без явного решения системы уравнений. В частности, необходимо выяснить, каким образом, зная функции d, и Ь, можно определить те виды, которые замещают другие и поэтому доминируют при больших временах.

Необходимый для этого качественный анализ динамики удается осуществить с помощью подстановок

где

– общее число частиц,

– нормированная возрастная структура i-ro рода. Рассмотрим сначала ситуацию, описываемую уравнением. Пользуясь подстановкой, получаем следующие уравнения для п, иpi:

и

Уравнение имеет в точности такую же структуру, как уравнение Эйгена, с тем лишь различием, что теперь приспособленность

– функционал нормированной возрастной структурыи поэтому может изменяться во времени.

Его временная эволюция определяется изменением во времени возрастное структуры, которая в свою очередь зависит от динамики чисел через уравнение. Зависимость приспособленности нормированной возрастной структуры приводит к тому, что виды могут повысить свои шансы на успех в ходе отбора за счетподходящего распределения особей по возрастным группам; иначе говоря, в ходе эволюции происходит замещение одних видов другими с оптимальной возрастное структурой. Каким образом по заданным функциям можно определить какие виды выживут в концеконцов? Чтобы ответить на этот вопрос, рассмотри стационарные решения уравнений и при больших временах

Мы получаем

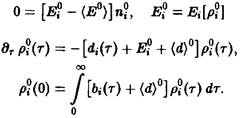
При рассмотрении уравнения Эйгена мы обнаружили, что уравнение допускает п различных стационарных решений вида

т.е. стационарны только такие ситуации, в которых все N особей представлены одним видом. С учетом соотношения из формулы следует, что

поэтому уравнение для замыкается. Таким образом, мы получаем:

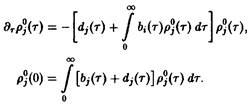
Вводя сокращенные обозначения

запишем уравнение в виде