Реферат: Индивидуальное развитие как новая стратегия эволюции

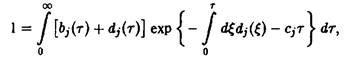
а также

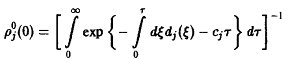
вследствие того, что по определению р,

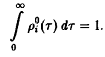
Тем самым мы полностью охарактеризовали стационарные решения систем уравнений. Можно показать, что при заданных и уравнение всегда допускает ровно одно решение

Величины Cjв силу соотношения определяют, поэтомуоднозначно определяются соотношением.

Из стационарных решений устойчиво только одно, и при t–* оо именно оно описывает поведение системы. Для этого решения справедливы неравенства

т.е. выживает вид, обладающий наибольшей приспособленностью. Соотношения – позволяют определить этот вид посредством формулы

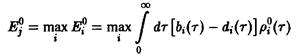
по известным функциям . Тем самым для системы конкурирующих видов с возрастной структурой, описываемой уравнением, становится возможным определять на основе заданных зависящих от возраста скорости воспроизведения и смертности тот из видов, который побеждает в ходе отбора. Используя соотношения, получаем

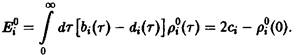
Можно показать, что

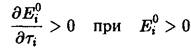
Таким образом, если мы ограничимся видами ст.е. такими, которые в отсутствие отбора сами не вымирают и то максимум величины достигается для того вида j, для которого величина также максимальна. Следовательно, доминирующий вид может определяться вместо соотношения соотношением

где с, – определяется формулой. Аналогичные соображения применимы и к модели (Эбелинг и др., 1986). Следует отметить, что в рассматриваемом случае соотношение получается и как определяющее уравнение для выживающего вида. Если воспользоваться определением параметров с, то соотношение можно рассматривать как разумное обобщение соотношения.

В заключение продемонстрируем важность внутривидовой возрастной структуры для процесса отбора на простом примере динамики, описываемой уравнением. Рассмотрим два вида с одинаковой и постоянной смертностью

и рождаемостью

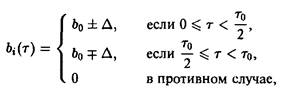
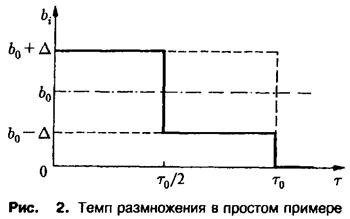
где в и в последующих соотношениях верхние знаки относятся к первому виду, а нижние – ко второму виду. Выбранные рождаемости представлены на рис. 2. Чтобы выяснить, какой вид побеждает в процессе отбора, необходимо исследовать, какая из определяемых соотношением величин с, больше. В рассматриваемом случае равенство упрощается до

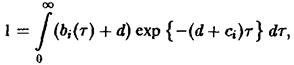
или

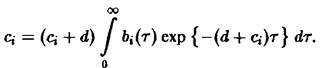
Отсюда с учетом формулы получаем