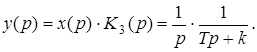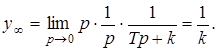Реферат: Интегральные методы оценки качества переходных процессов
![]() (6)
(6)
Подинтегральное выражение – z 2 ( t ) всегда положительно не зависимо от знака функции z ( t ) .
Определим J 2 без расчета переходного процесса, для этого воспользуемся дуальной теоремой.
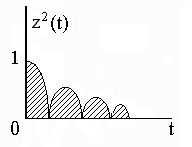
Рис. 4
Основная теорема : произведению изображений соответствует свертка оригиналов
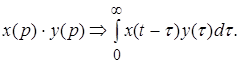 (7)
(7)
Дуальная теорема : произведению оригиналов соответствует свертка изображений
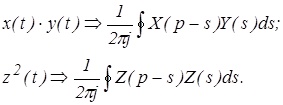 (8)
(8)
Так как 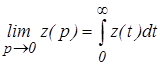 ,
,
то можно получить следующую формулу для расчета квадратичной интегральной оценки
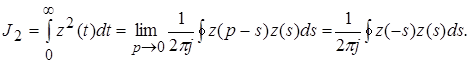 (9)
(9)
Этот интеграл можно вычислить либо с помощью вычетов по полюсам подинтегральной функции, либо с использованием табулированных значений интеграла для функции
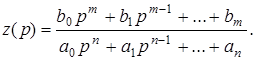 (10)
(10)
В таблице 1 приведены табулированные значения интеграла для n = 1 ¸ 3 для систем более высокого порядка таблицы приведены в литературе [5].
Таблица 1
| n | J2 |
| 1 | |
| 2 | |
| 3 |
Недостаток метода. Рассмотрим переходные процессы (рис. 5).
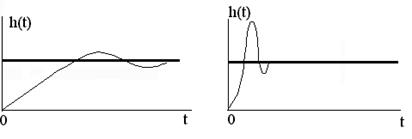
а) б)
Рис. 5
При использовании этого метода два процесса могут иметь одинаковую площадь регулирования, но оба они плохие по различным показателям качества, у первого большое время регулирования, а во втором большое перерегулирование.
Пример 6.Вычислить величину J2 для заданной системы (рис. 6).
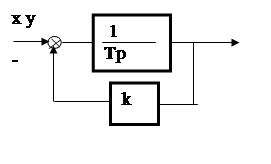 | |
|
Рис. 6
3. Определим z(p)
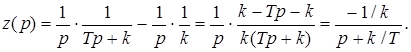
4. Определим величину интеграла J2 с помощью вычетов s1 = – k/T
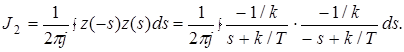
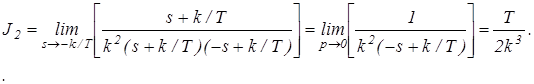
5. Определим величину интеграла J2 с помощью таблиц