Реферат: Интуитивное понятие алгоритма и его свойств
Алгоритм отностится к основным понятиям математики, а поэтому не имеет определения. Часто это понятие формулируют так:"точное предписание о порядке выполнения действий, из заданного фиксированного множества, для решения всех задач, заданного класса".
Рассмотрим подробнее ключевые слова в этой формулировке:
"точное предписание” означает, что предписание однозначно и одинаково понимается всеми исполнителями алгоритма и при одних и тех же исходных данных любой исполнитель всегда получает один и тот же результат;
“из заданного фиксированного множества” означает, что множество действий, используемых в предписании, оговорено заранее и не может меняться в ходе исполнения алгоритма.
“решения всех задач, заданного класса” означает, что это предписание предназначено для решения класса задач, а не одной отдельной задачи. Позднее мы подробнее рассмотрим смысл выражения “класс задач”.
Эта формулировка требует знания таких понятий, как исходные данные, результат, действие, исполнитель, класс задач. Познакомимся с ними на примере алгоритма Евклида нахождения наибольшего общего делителя (НОД) двух натуральных чисел:
Исходные данные: n, m - натуральные числа
Результат: НОД (n, m) - натуральное число d, такое, что
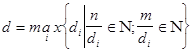
Алгоритм:
1. Положи a =n, b = m ; (следующий шаг)
2. Сравни a и b ; (следующий шаг)
3. Если a=b, то a - результат; (стоп)
иначе; (следующий шаг)
4. Если a<b, то поменяй их местами; (следующий шаг)
5. Вычти b из a ; (следующий шаг)
6. Положи a = разность; (перейти к шагу 2)
В этом алгоритме действия обозначены словами: положи, сравни, если_то_иначе, вычти, поменяй_местами, следующий шаг. Все исполнители, реализующие этот алгоритм, должны одинаково понимать смысл этих действий.
Например:
Сравни a и b ;(следующий шаг)
Все исполнители должны “понимать”, что надо сравнить значения, представленные символами а и b, а не сами символы, и перейти к действию 3.
Положи a = разность; (перейти к шагу 2)
Означает, что в качестве текущего значения переменной а надо взять разность между значениями, представленными переменными а и b, вычисленную на предыдущем этапе, и перейти к действию 2.
Последовательность действий, выполняемых исполнителем, образуют процесс. Назовем этот процесс вычислительным процессом. Например, для случая исходных данных n=3, m=2 и алгоритма НОД этот процесс можно описать так:
| значение а | значение b | № действия | |
| 1 | 3 | 2 | 1 |
| 2 | 3 | 2 | 2 |
| 3 | 3 | 2 | 3 |
| 4 | 3 | 2 | 4 |
| 5 | 3 | 2 | 5 |
| 6 | 1 | 2 | 6 |
| 7 | 1 | 2 | 2 |
| 8 | 1 | 2 | 3 |
| 9 | 2 | 1 | 4 |
| 10 | 2 | 1 | 5 |
| 11 | 1 | 1 | 6 |
| 12 | 1 | 1 | 2 |
| 13 | 1 | 1 | 3 |
Стоп
Нетрудно видеть разницу между алгоритмом и вычислительным процессом, им порождаемым. Так, например, действие, которое встречается в алгоритме один раз, может быть выполнено несколько раз, а следовательно встретиться неоднократно в описании вычислительного процесса. Примерами такого действия может быть действие 3, либо действие 5, либо 6. В нашем алгоритме, как правило, экземпляры одного и того же действия будут различаться данными (операндами), над которыми совершается это действие. Однако, эти данные могут быть представлены одними и теми же именами.
По алгоритму не всегда можно предсказать вычислительный процесс. Например, не всегда можно предвидеть точно, как много действий будет в вычислительном процессе. Примером тому может служить алгоритм вычисления НОД.
Алгоритм всегда определяет однозначно, какое действие должно быть выполнено следующим, равно как и то, какое действие должно быть выполнено первым. Очередное действие всегда определено однозначно. Именно этой цели служат слова “(cледующий шаг).” Они явно указывают какое действие должно быть выполнено следующим. В силу этого свойства алгоритма, которое называется детерминированность, вычислительный процесс всегда для заданных исходных данных определен однозначно. Таким образом, при одних и тех же исходных данных вычислительный процес будет одним и тем же.
Обычно по умолчанию предполагают “естественный” порядок выполнения действий в алгоритме. Это означает, что если нет явного изменения порядка выполнения действий, то они выполняются последовательно одно за другим, а выполнение алгоритма начинают с первого по порядку действия. Поэтому, в дальнейшем слова “(следующий шаг)” мы будем опускать.
--> ЧИТАТЬ ПОЛНОСТЬЮ <--