Реферат: Использование дифференциальных уравнений, передаточных и частотных передаточных функций
 ,
,
отсюда найдем х2
 ,
,
где W(s) – передаточная функция ─ реакция системы на входное воздействие в области изображений Лапласа.
Таким образом, передаточная функция W(s) определяется как отношение изображений по Лапласу выходной и входной величин при нулевых начальных условиях.
В последующем изложении W(s) и W(p) мы будем именовать передаточной функцией, имея в виду, что s- комплексная переменная, а p- оператор дифференцирования.
В данном случае мы получили алгебраическую форму записи ДУ. Формально она может быть получена из упрощенной символической формы заменой оператора дифференцирования на переменную s и оригиналов на изображения:

Для нахождения оригинала может быть использовано обратное преобразование Лапласа:
 .
.
Обратное преобразование выполняют путем разложения изображения на простейшие дроби и последующего использования таблиц.
Использование переходной и весовой функций
Переходной функцией называют реакцию системы на ступенчатую единичную функцию, которую определяют как 1(t) (рис. 3.1):
 .
.

Рис. 1. Единичная ступенчатая функция
Переходная функция используется при исследовании переходных режимов следящих систем. Переходная характеристика – графическое изображение переходной функции. Типовые переходные характеристики следящих систем изображены на рис. 2.
Устойчивые системы

Неустойчивые системы

Рис. 2. Переходные характеристики
Переходная характеристика может быть найдена аналитически. Запишем реакцию системы на 1(t) в виде ДУ в сокращенной форме:
![]() ,
,
где W(p) – операторный коэффициент передачи.
Перейдя в область изображений по Лапласу, получим следующие выражения:
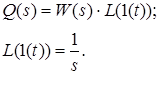
Осуществив обратное преобразование Лапласа, получим переходную функцию q(t).
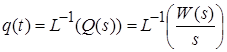 .
.
Весовая функция (импульсная характеристика) – реакция системы на воздействие в виде δ-функции, определяемой как
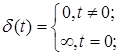
![]() .
.