Реферат: Использование дифференциальных уравнений, передаточных и частотных передаточных функций

;

.

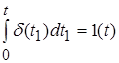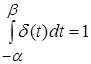Весовая функция h(t) равна:

.

Переходя в область изображений, получим следующие выражения:

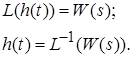
Таким образом, весовая и передаточная функции связаны преобразованием Лапласа.

Весовая функция используется для определения выходной величины с помощью интеграла Дюамеля:

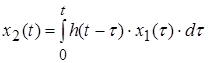. (3)

В соответствии с условием физической реализуемости: реакция системы на входное воздействие появляется не раньше воздействия, т. е

, при t<0,

можно записать:

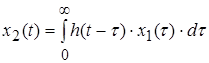. (4)

Для определения установившегося значения можно полагать, что воздействие началось в момент и для расчета использовать выражение:

.

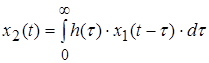Использование частотных передаточных функций

Частотная передаточная функция (комплексный коэффициент передачи) определяет реакцию системы на гармоническое входное воздействие и используется для анализа следящих систем. Ее можно найти, используя ДУ (3.1), если полагать, что – гармоническое воздействие в комплексной форме определяется выражением

, (5)

где - комплексная амплитуда.

Будем искать частное решение неоднородного ДУ (1) в виде:

, (6)

где .

Подставляя (3.5), (3.6) в (3.1) и учитывая, что

,

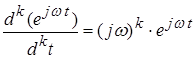получим:

,

где 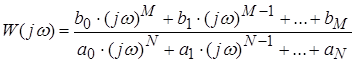─ частотная передаточная функция (комплексный коэффициент передачи).

Частная передаточная функция – это отношение комплексных амплитуд входных и выходных гармонических воздействий при нулевых начальных условиях.

W(jω) можно получить формально из W(s), заменой s на jω.

W(jω)можно представить а показательной и алгебраической форме: