Реферат: Использование цепей Маркова в моделировании социально экономических процессов

- она получает доход ;

- ее состояние в следующий момент времени определяется вероят­ностью , где - вероятность того, что система из состояния при выборе решения перейдет в состояние .

Таким образом, смысл -го решения в i-м состоянии заклю­чается в выборе одного набора переходных вероятностей из возможных. Предполагается, что доход ограничен при всех и .

Кроме того,

, при всех и .

Управляемой цепью Маркова называется конструкция, зада­ваемая параметрами , где К- решения, Р -вероятности переходов, r -доходы. Доход, полученный за несколько шагов, является случайной величиной, зависящей от начального состоя­ния и принимаемых в каждый момент времени решений.

Назовем решение, принимаемое в конкретный момент, частным управлением. Тогда управление есть последовательность решений в моменты n = 1, 2, ... Качество управления можно оценить сред­ним суммарным доходом (при конечном времени) или среднем дохо­дом в единицу времени (при бесконечном времени).

Пусть (2)

Стратегией называется последовательность решений

где - вектор вида (2), i-я компонента которого, обозначаемая через , является решением, принимаемым в состоянии в момент п. Другими словами, задание стратегии означает пол­ное описание в каждый момент времени t =1, 2, ..., п, ... конкретных решений, которые должны были бы приниматься в i-м состоянии , если бы система находилась в нем в рассматриваемый момент.

Стратегия обозначается через и назы­вается стационарной. Стратегия называется мар­ковской, если решение , принимаемое в каждом конкретном сос­тоянии, не зависит от предшествующих состояний и принимавшихся в них решений. В случае марковской стратегии решения могут зависеть только от момента времени п.

Обозначим произвольную конечную часть стратегии через . Пусть зафиксированы произвольная стратегия некоторый момент времени п. Если в этот момент система находилась в состоянии , то в следующий (п+1)- й момент времени она будет находиться в состоянии с вероятностью , где . Тогда матрица переходных ве­роятностей в момент п имеет вид

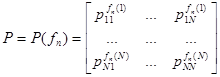
Таким образом, при фиксированной стратегии получаем цепь Маркова с матрицами перехода

Обозначим - вектор суммарных средних доходов, полученных до любого момента n включительно, для некоторой стратегии . Стратегия максимизирующая , то есть удовлетворяющая неравенству

≥ при любых

называется оптимальной

Верны следующее утверждения:

Утверждение 1. Для бесконечного времени существует опти­мальная стационарная стратегия.

Утверждение 2. Для конечного времени существует оп­тимальная марковская стратегия.

Таким образом, решение (при бесконечном времени) зависит только от состояния, в котором находится система, и не зависит ни от момента времени, ни от всей предыдущей траектории последовательности состояний и принятых решений). В случае ко­нечного времени оптимальная стратегия является марковской, т. е. может зависеть еще и от момента времени принятия решения.

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ:

1. «Теория выбора и принятия решений»: учебное пособие. И.М. Макаров, Т.М.

Виноградская, А.А. Рубчинский, В.Б. Соколов. Москва, изд. «Наука», 1982.

2. «Теория вероятностей» Е.С. Вентцель. Москва, изд. «Наука», 1969.