Реферат: Исследование риска в автотранспортном страховании

Теперь необходимо проверить возможность аппроксимации урегулированных убытков отрицательным биномиальным законом .

Случайная величина Х имеет отрицательное биномиальное распределение с параметрами (r , p ), если в последовательности испытаний Бернулли с вероятностью успеха р и вероятностью неудачи q =1- p вероятность числа неудач k , происшедших до a -го успеха, определяется по формуле:

,

где r - число успехов, целое положительное число;

k - число неудач, происшедших до числа успехов a .

Числовые характеристики отрицательного биномиального распределения:

,

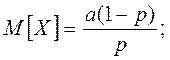
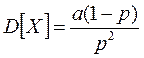из формул (2) получили формулы для оценки параметров p и a :

; .

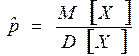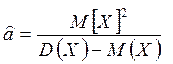Очевидно, что это распределение применимо, только если математическое ожидание изучаемой случайной величины не превышает дисперсии, иначе вероятность получается больше 1.

После подсчета М(Х) и D(X) рассчитаем оценки параметров для отрицательного биномиального распределения по формулам приведенным выше. Результаты запишем в Таблицу 3.

Таблица 3

i	mi	M(x)	M(x2 )	D(x)	p	a	Pn (mi )
0	5242	0,022922	0,023668	0,022362	1,0250	0,938	#ЧИСЛО!
1	123
2	1
N	5366

Видно, что т.к. математическое ожидание изучаемой случайной величины превышает дисперсию, вероятность получилась больше 1, значит, применение отрицательного биномиального распределения невозможно.

Это можно проверить, если применить функцию ОТРБИНОМРАСП.

В результате примения данной функции, получилось, что вероятность_успеха > 1 и число_успехов < 1, следовательно, функция возвращает значение ошибки #ЧИСЛО! Отрицательное биномиальное распределение в этом примере не приемлемо.

II. Исследование распределения величины ущерба

при наступлении одного страхового случая

Для дальнейшей обработки данных необходимо отобрать все урегулированные убытки, произошедшие в 2003 году. Для этого надо воспользуемся командой фильтр, и в столбце «Сумма фактически выплаченного возмещения» поставить условие «не равно 0». После отбора всех сумм фактически выплаченного возмещения в 2003 году, необходимо скопировать этот столбец в ППП Statistica 6.0.

Рассмотрим анализ величины ущерба в группе ГО в 2003 году. Для этого необходимо проверить возможность аппроксимации данной величины непрерывными законами распределения: нормальным, логнормальным, экспоненциальным и гамма - распределением.

2.1. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ

Непрерывная случайная величина Х имеет нормальное распределение (распределена по нормальному закону)(1), если плотность распределения вероятности f(x) имеет вид:

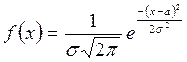
где а и s —некоторые постоянные, называемые параметрами нормального распределения.

Функция распределения F(x) в рассматриваемом случае принимает вид:

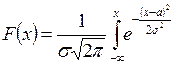
Параметр а - есть математическое ожидание случайной величины, имеющей нормальное распределение, s - среднее квадратическое отклонение, тогда дисперсия равна:

Выберем в окне пункт «Continuous distributions» (Непрерывные распределения), что означает выбор непрерывного распределения, и необходимое распределение: «Normal». Результаты проверки на нормальное распределение приведены в Таблице 4 и на Графике 1.

Таблица 4

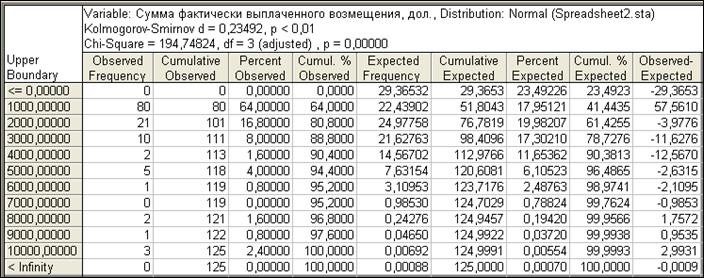
По полученным результатам можно сделать вывод о том, что эмпирические частоты не совпадают с полученными теоретическими. Рассмотрим График 1.

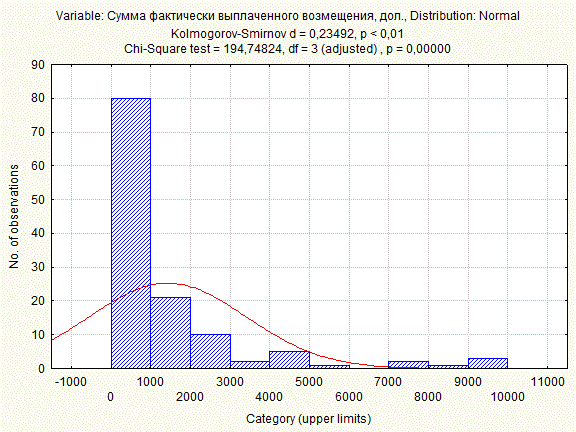
График 1. Проверка на нормальное распределение

При рассмотрении Графика 1 приходим к этому же выводу.

Сравним также эмпирические данные с полученными теоретическими с помощью критерия Колмогорова-Смирнова и критерия c² .

Критерий Колмогорова-Смирнова тест

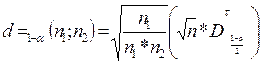
С помощью критерия Колмогорова-Смирнова необходимо проверить гипотезу о том, что величина размера ущерба распределена по нормальному закону. Для этого необходимо сравнить d_набл. и d_крит при заданном уровне a , а затем принять или отвергнуть гипотезу.

d_крит находится по таблицам распределения Колмогорова-Смирнова, а при большом числе договоров (n>100) по асимптотическим формулам:

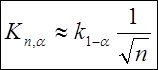где k_1-α - квантиль порядка 1-α распределения Колмогорова, которые находят по таблице:

Асимптотические критические значения k_1-α для статистик Колмогорова и Смирнова-Колмогорова

α	0,2	0,1	0,05	0,02	0,01
k1-α	1,073	1,224	1,358	1,517	1,628

Кроме того, расчёт d_крит возможен при n→∞ по асимптотическому соотношению:

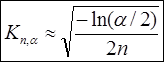В рассматриваемом примере n=125, a=0.05, расчёты по приведённым асимптотическим формулам приводят к d_крит = 0,121463 по 1-й формуле и d_крит = 0,121463 по 2-й формуле.

d_набл =0,23, и d_набл >d_крит =0,115 при a=0,05, т.е. гипотеза о нормальном законе распределения отвергается.

Далее необходимо аналогично проверить возможность аппроксимации других распределений – логнормального, экспоненциального и гамма-распределения.