Реферат: Исследование риска в автотранспортном страховании

Далее необходимо аналогично проверить возможность аппроксимации других распределений – логнормального, экспоненциального и гамма-распределения.

2.2. ЛОГНОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ

Осуществим проверку на логнормальное распределение. Случайная величина X имеет логарифмическое нормальное (логнормальное) распределение (1) с параметрами a и σ , если случайная величина ln x имеет нормальное распределение с параметрами a > 0 и σ . Функция плотности вероятностей p (x ), функция распределения F (x ) и моменты M( X ) , D( X ) логнормального распределения имеют, соответственно, вид:

; , .

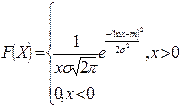Таблица 5

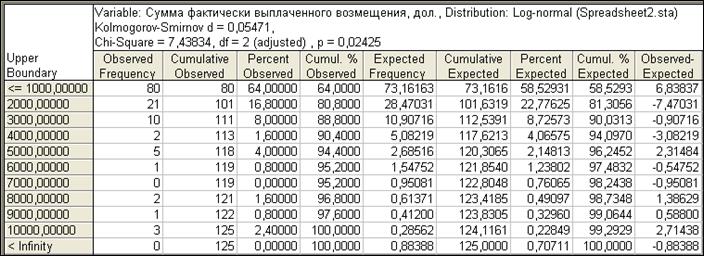
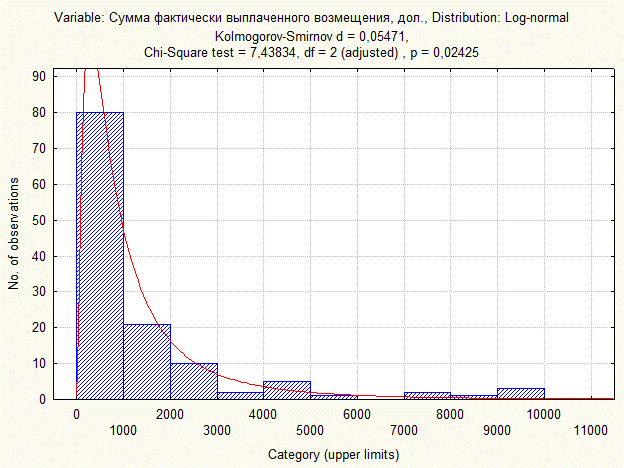
График 2. Проверка на логнормальное распределение

Сравним эмпирические данные с полученными теоретическими с помощью критерия Колмогорова-Смирнова и критерия c² . Kolmogorov-Smirnov d = 0,05471

d _набл < d _крит =0,121 при a =0,05, т.е. гипотеза о том, что данная совокупность распределена по логнормальному закону, не отвергается. Следовательно, для этого примера можно считать адекватным логнормальное распределение.

2.3. ЭКСПОНЕНЦИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ

Осуществим проверку на экспоненциальное распределение.

; , .

Таблица 6

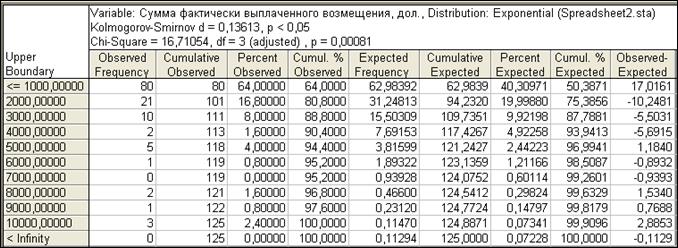
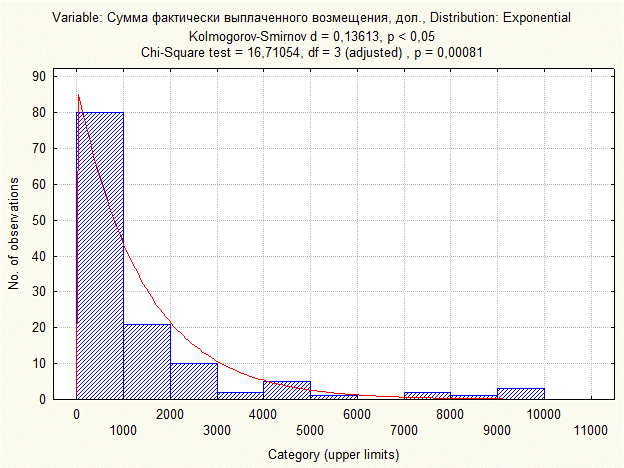График 3. Проверка на экспоненциальное распределение

Сравним эмпирические данные с полученными теоретическими с помощью критерия Колмогорова-Смирнова и критерия c² . Kolmogorov-Smirnov d = 0,13613, p < 0,05

d _набл > d _крит =0,121 при a =0,05, т.е. гипотеза о том, что данная совокупность распределена по экспоненциальному закону, отвергается.

2.4. ГАММА РАСПРЕДЕЛЕНИЕ

Осуществим проверку на гамма распределение.

, , .

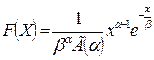Таблица 7

График 4. Проверка на гамма распределение

Сравним эмпирические данные с полученными теоретическими с помощью критерия Колмогорова-Смирнова и критерия c² . Kolmogorov-Smirnov d = 0,13633, p < 0,05

d _набл > d _крит =0,121 при a =0,05, т.е. гипотеза о том, что данная совокупность распределена по закону гамма распределения, отвергается.

Выводы .

1. Проанализировав распределение числа убытков в одном договоре на соответствие двум законам распределения, Пуассоновскому и отрицательному биномиальному, было определено на основе c² , что для рассматриваемого примера адекватной признается пуассоновская модель.

Отрицательное биномиальное распределение в этом примере не приемлемо т.к. математическое ожидание изучаемой случайной величины превышает дисперсию, а также вероятность_успеха > 1 и число_успехов < 1.

2. Исследуя распределение величины ущерба при наступлении одного страхового случая, было определено на основе анализа теоретических и эмпирических частот, а также критерия Колмогорова-Смирнова, что гипотеза о том, что данная совокупность распределена по логнормальному закону, не отвергается. Следовательно, для этого примера можно считать адекватным логнормальное распределение.

Согласованность эмпирических и теоретических частот, рассчитанных с помощью логнормального распределения, изобразим на Графике 5.

График. 5. Согласованность эмпирических и теоретических частот, рассчитанных с помощью логнормального распределения

График 5 подтверждает справедливость того, что данная совокупность подчинена логнормальному распределению.