Реферат: Исследование согласованного фильтра
где |K(jw)| - амплитудно-частотная характеристика фильтра; Y(w) - фазовая характеристика фильтра.
Сравнивая (15) и (16) находим

Из (17) следует, что амплитудно частотная характеристика согласованного фильтра с точностью до постоянной совпадает с амплитудным спектром сигнала.
Фазовая характеристика согласованного фильтра определяется двумя слагаемыми. Первое из них - j(w) равно фазовому спектру сигнала, взятому с противоположным знаком. Назначение его в том чтобы компенсировать фазовые сдвиги различных составляющих сигнала. В результате в некоторый момент времени t=t0 все составляющие выходного сигнала будут совпадать по фазе и, складываясь, давать максимум выходного сигнала. Если бы фазовая характеристика фильтра не компенсировала фазовые сдвиги составляющих сигнала, то максимумы гармонических составляющих сигнала не совпадали бы во времени, а это привело бы к уменьшению выходного напряжения.
Второе слагаемое - wt0 обеспечивает задержку момента совпадения фаз составляющих сигнала на величину t0 . Понятно, что значение t0 не может быть меньше длительности обрабатываемого сигнала.
Напряжение на выходе согласованного фильтра

Из (19) следует, что выходное напряжение определяется только амплитудным спектром сигнала и не зависит от фазового спектра. Это объясняется тем, что взаимные фазовые сдвиги составляющего сигнала скомпенсированы фазовой характеристикой фильтра.
Максимальное значение uвых (t) принимает в момент времени t=t0 .. Еще раз подчеркнем, что значение t0 должно быть больше или равно длительности сигнала, т.е. максимум uвых (t) достигается только после обработки всего принятого сигнала.
Рассмотрим импульсную характеристику h(t) согласованного фильтра. Учитывая, что h(t) любого фильтра связано K(jw) преобразованием Фурье, находим

Из выражения (20) следует, что импульсная характеристика согласованного фильтра является зеркальным отображением сигнала ts(t) относительно прямой t=t0 /2 (рис.1).

Рисунок 1
Учитывая условие физической реализуемости фильтра h(t)=0 при t<0, обнаруживаем, что
| s(t0 -t)=0 | при t<0 | (21) |
| s(t)=0 | при t>t0 |
Условие (21) показывает, что значение t0 надо выбирать большим или равным длительности сигнала tc . На практике обычно для уменьшения реакции фильтра берут t0 =tc .
Найдем формулу напряжения на выходе фильтра, для этого воспользуемся интегралом Дюамеля:

С учетом (20) получаем
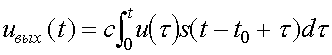
В момент времени t=t0
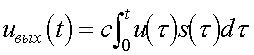
Видно, что выражение (24) совпадает с выражением (1), т.е. согласованный фильтр, как и корреляционный приемник, вычисляет взаимную корреляцию принятого и полезного сигналов. Если при корреляционном приеме копия ожидаемого сигнала вырабатывается на приемной стороне с помощью специального генератора, то при согласованной фильтрации информация о сигнале заключена в комплексно-частотной характеристике.
Если перенести начало отсчета времени в точку t=t0 , то из (23)
![]()
т.е. напряжение на входе согласованного фильтра в отсутствии помех совпадает с корреляционной функцией полезного сигнала.
В заключение отметим, что согласованный фильтр, в отличии от корреляционного приемника обладает свойствами инвариантности относительно момента прихода сигнала. Фильтр, согласованный с некоторым сигналом s(t), имеет импульсную характеристику, определенную выражением (20), Очевидно, что этот же фильтр будет согласованным с сигналом s(t-t1 ), сдвинутым по времени относительно s(t) на t1 . Изменение времени прихода сигнала приводит только к смещению момента достижения выходным сигналом его максимального значения.
Согласованный фильтр для М-сигналов
Формирование М-сигналов. В последнее время в радиолокации и связи все более широко применяются сложные широкополосные сигналы. Одним из способов получения таких сигналов является изменение фазы высокочастотных колебаний по закону М-последовательностей, строящихся , в свою очередь на основе линейных рекуррентных последовательностей.
Линейной рекуррентной последовательностью называется периодическая последовательность символов x1 ?x2 ...xn ,...xi ,...xL , удовлетворяющая рекуррентному правилу
![]()
где символы последовательности и коэффициенты ai принимают значения из области G(0,1....p-1), сложение и умножение производится по модулю р. Здесь число n - память последовательности, число р - основание последовательности, а наименьшее число L, при котором xL+i =xi - период, или длинна последовательности. Коэффициент а в дальнейшем будем считать равным нулю.
Соотношение (25) называется правилом кодирования. В случае двоичной последовательности значения символов последовательности и коэффициентов ai равны либо нулю, либо единице, а суммирование ведется по MOD 2, которое определяется так
| 0Å0=0 | 0Å1=1 |
| 1Å0=1 | 1Å1=0 |
Из определения линейной зависимости рекуррентной последовательности вытекает, что для ее построения необходимо знать первые n членов последовательности и правило кодирования ,т.е. уравнение (25)
Пример. Пусть р=2, n=4, начальное слово 1111, правило кодирования x1 =xi-3 Åxi-4 . Тогда x5 =x2 Åx1 =1Å1=0, x6 =x3 Åx2 =1Å1=0.
По уравнению (25) нетрудно представить и схемную реализацию устройства, генерирующего последовательность. Оно должно содержать блок памяти предназначенный, для запоминания n последних выбранных членов последовательности, и комбинационную схему, работа которой определяется заданным правилом кодирования.
На рис. 2 представлена функциональная схема генератора линейной рекуррентной последовательности.
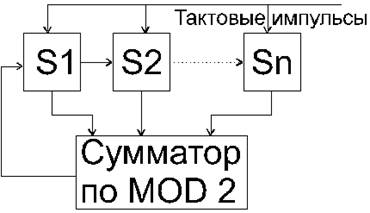
Рисунок 2
Генератор состоит из n триггеров, выполняющих роль элементов памяти и устройства обратной связи, описываемого некоторой булевой функцией
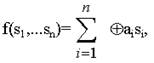
где si - состояние i-й ячейки памяти (i-го триггера), принимающего значение 0 или 1. Триггеры соединены между собой таким образом, что образуют регистр сдвига.